Persamaan Kuadratik
Persamaan kuadratik adalah polinomial urutan kedua dengan 3 pekali - a , b , c .
Persamaan kuadratik diberikan oleh:
ax 2 + bx + c = 0
Penyelesaian untuk persamaan kuadratik diberikan oleh 2 nombor x 1 dan x 2 .
Kita boleh mengubah persamaan kuadratik ke bentuk:
( x - x 1 ) ( x - x 2 ) = 0
Formula Kuadratik
Penyelesaian untuk persamaan kuadratik diberikan oleh formula kuadratik:
![]()
Ungkapan di dalam akar kuadrat disebut diskriminan dan dilambangkan dengan Δ:
Δ = b 2 - 4 ac
Formula kuadratik dengan notasi diskriminasi:
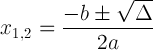
Ungkapan ini penting kerana dapat memberitahu kita tentang penyelesaiannya:
- Apabila Δ/ 0, terdapat 2 punca sebenar x 1 = (- b + √ Δ ) / (2a) dan x 2 = (- b-√ Δ ) / (2a) .
- Apabila Δ = 0, terdapat satu punca x 1 = x 2 = -b / (2a) .
- Apabila Δ <0, tidak ada punca sebenar, terdapat 2 punca kompleks:
x 1 = (- b + i√ -Δ ) / (2a) dan x 2 = (- bi√ -Δ ) / (2a) .
Masalah # 1
3 x 2 +5 x +2 = 0
penyelesaian:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
Masalah # 2
3 x 2 -6 x +3 = 0
penyelesaian:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
Masalah # 3
x 2 +2 x +5 = 0
penyelesaian:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
Tidak ada penyelesaian sebenar. Nilai adalah nombor kompleks:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
Graf Fungsi Kuadratik
Fungsi kuadratik adalah fungsi polinomial urutan kedua:
f ( x ) = ax 2 + bx + c
Penyelesaian untuk persamaan kuadratik adalah akar fungsi kuadratik, yang merupakan titik persimpangan grafik fungsi kuadratik dengan paksi-x, ketika
f ( x ) = 0
Apabila terdapat 2 titik persilangan grafik dengan paksi-x, terdapat 2 penyelesaian untuk persamaan kuadratik.
Apabila terdapat 1 titik persilangan grafik dengan paksi-x, terdapat 1 penyelesaian untuk persamaan kuadratik.
Apabila tidak ada titik persilangan grafik dengan paksi-x, kita tidak mendapat penyelesaian sebenar (atau 2 penyelesaian kompleks).