Peraturan Logaritma
Yang asas b logaritma nombor adalah eksponen yang kita perlu meningkatkan asas untuk mendapatkan nombor.
- Definisi logaritma
- Peraturan logaritma
- Masalah logaritma
- Logaritma kompleks
- Graf log (x)
- Jadual logaritma
- Kalkulator logaritma
Definisi logaritma
Apabila b dinaikkan ke daya y sama x:
b y = x
Maka logaritma asas b adalah sama dengan y:
log b ( x ) = y
Contohnya apabila:
2 4 = 16
Kemudian
log 2 (16) = 4
Logaritma sebagai fungsi songsang fungsi eksponensial
Fungsi logaritma,
y = log b ( x )
adalah fungsi songsang fungsi eksponensial,
x = b y
Oleh itu, jika kita mengira fungsi eksponen logaritma x (x/ 0),
f ( f -1 ( x )) = b log b ( x ) = x
Atau jika kita mengira logaritma fungsi eksponen x,
f -1 ( f ( x )) = log b ( b x ) = x
Logaritma semula jadi (ln)
Logaritma semula jadi adalah logaritma ke pangkalan e:
ln ( x ) = log e ( x )
Apabila pemalar e adalah nombor:
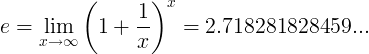
atau
![]()
Lihat: Logaritma semula jadi
Pengiraan logaritma terbalik
Logaritma songsang (atau anti logaritma) dikira dengan menaikkan asas b ke logaritma y:
x = log -1 ( y ) = b y
Fungsi logaritma
Fungsi logaritma mempunyai bentuk asas:
f ( x ) = log b ( x )
Peraturan logaritma
| Nama peraturan | Peraturan |
|---|---|
Peraturan produk logaritma |
log b ( x ∙ y ) = log b ( x ) + log b ( y ) |
Peraturan hasil bagi logaritma |
log b ( x / y ) = log b ( x ) - log b ( y ) |
Peraturan kuasa logaritma |
log b ( x y ) = y ∙ log b ( x ) |
Peraturan suis asas logaritma |
log b ( c ) = 1 / log c ( b ) |
Peraturan perubahan asas logaritma |
log b ( x ) = log c ( x ) / log c ( b ) |
Derivatif logaritma |
f ( x ) = log b ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( b )) |
Integrasi logaritma |
∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C |
Logaritma nombor negatif |
log b ( x ) tidak ditentukan apabila x ≤ 0 |
Logaritma 0 |
log b (0) tidak ditentukan |
Logaritma 1 |
log b (1) = 0 |
Logaritma asas |
log b ( b ) = 1 |
Logaritma tak terhingga |
lim log b ( x ) = ∞, apabila x → ∞ |
Lihat: Peraturan logaritma
Peraturan produk logaritma
Logaritma pendaraban x dan y adalah jumlah logaritma x dan logaritma y.
log b ( x ∙ y ) = log b ( x ) + log b ( y )
Sebagai contoh:
log 10 (3 ∙ 7) = log 10 (3) + log 10 (7)
Peraturan hasil bagi logaritma
Logaritma pembahagian x dan y adalah perbezaan logaritma x dan logaritma y.
log b ( x / y ) = log b ( x ) - log b ( y )
Sebagai contoh:
log 10 (3 / 7) = log 10 (3) - log 10 (7)
Peraturan kuasa logaritma
Logaritma x dinaikkan kepada daya y adalah y kali ganda daripada logaritma x.
log b ( x y ) = y ∙ log b ( x )
Sebagai contoh:
log 10 (2 8 ) = 8 ∙ log 10 (2)
Peraturan suis asas logaritma
Logaritma asas b ialah 1 dibahagikan dengan logaritma asas
log b ( c ) = 1 / log c ( b )
Sebagai contoh:
log 2 (8) = 1 / log 8 (2)
Peraturan perubahan asas logaritma
Asas b logaritma x ialah asas c logaritma x dibahagi dengan asas c logaritma b.
log b ( x ) = log c ( x ) / log c ( b )
Sebagai contoh, untuk mengira log 2 (8) dalam kalkulator, kita perlu menukar asas menjadi 10:
log 2 (8) = log 10 (8) / log 10 (2)
Lihat: peraturan perubahan asas log
Logaritma nombor negatif
Logaritma asas b asas x apabila x <= 0 tidak ditentukan apabila x negatif atau sama dengan sifar:
log b ( x ) tidak ditentukan apabila x ≤ 0
Lihat: log nombor negatif
Logaritma 0
Logaritma asas b sifar tidak ditentukan:
log b (0) tidak ditentukan
Had logaritma asas b, apabila x menghampiri sifar, adalah minus tak terhingga:
![]()
Lihat: log sifar
Logaritma 1
Logaritma asas b adalah sifar:
log b (1) = 0
Sebagai contoh, asas dua logaritma satu adalah sifar:
log 2 (1) = 0
Lihat: log satu
Logaritma tak terhingga
Had logaritma asas b x, apabila x mendekati tak terhingga, sama dengan tak terhingga:
lim log b ( x ) = ∞, apabila x → ∞
Lihat: log infiniti
Logaritma asas
Logaritma asas b adalah satu:
log b ( b ) = 1
Sebagai contoh, asas dua logaritma dua adalah satu:
log 2 (2) = 1
Derivatif logaritma
Bila
f ( x ) = log b ( x )
Maka terbitan f (x):
f ' ( x ) = 1 / ( x ln ( b ))
Lihat: derivatif log
Logaritma kamiran
Kamiran logaritma x:
∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C
Sebagai contoh:
∫ log 2 ( x ) dx = x ∙ (log 2 ( x ) - 1 / ln (2) ) + C
Penghampiran logaritma
log 2 ( x ) ≈ n + ( x / 2 n - 1),
Logaritma kompleks
Untuk nombor kompleks z:
z = re iθ = x + iy
Logaritma kompleks akan (n = ...- 2, -1,0,1,2, ...):
Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))
Masalah dan jawapan logaritma
Masalah # 1
Cari x untuk
log 2 ( x ) + log 2 ( x -3) = 2
Penyelesaian:
Menggunakan peraturan produk:
log 2 ( x ∙ ( x -3)) = 2
Menukar bentuk logaritma mengikut definisi logaritma:
x ∙ ( x -3) = 2 2
Atau
x 2 -3 x -4 = 0
Menyelesaikan persamaan kuadratik:
x 1,2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4, -1
Oleh kerana logaritma tidak ditentukan untuk nombor negatif, jawapannya adalah:
x = 4
Masalah # 2
Cari x untuk
log 3 ( x +2) - log 3 ( x ) = 2
Penyelesaian:
Menggunakan peraturan bagi:
log 3 (( x +2) / x ) = 2
Menukar bentuk logaritma mengikut definisi logaritma:
( x +2) / x = 3 2
Atau
x +2 = 9 x
Atau
8 x = 2
Atau
x = 0.25
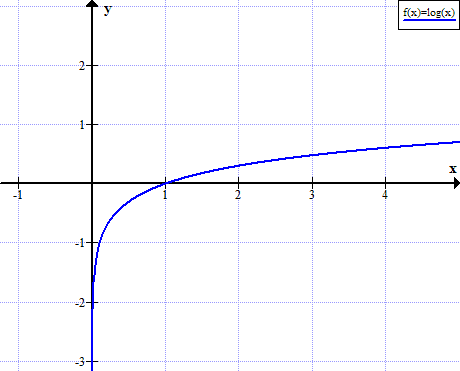
Graf log (x)
log (x) tidak didefinisikan untuk nilai bukan positif sebenar x:
Jadual logaritma
| x | log 10 x | log 2 x | log e x |
|---|---|---|---|
| 0 | tidak ditentukan | tidak ditentukan | tidak ditentukan |
| 0 + | - ∞ | - ∞ | - ∞ |
| 0.0001 | -4 | -13.287712 | -9.210340 |
| 0.001 | -3 | -9.965784 | -6.907755 |
| 0.01 | -2 | -6.643856 | -4.605170 |
| 0.1 | -1 | -3.321928 | -2.302585 |
| 1 | 0 | 0 | 0 |
| 2 | 0.301030 | 1 | 0.693147 |
| 3 | 0.477121 | 1.584963 | 1.098612 |
| 4 | 0.602060 | 2 | 1.386294 |
| 5 | 0.698970 | 2.321928 | 1.609438 |
| 6 | 0.778151 | 2.584963 | 1.791759 |
| 7 | 0.845098 | 2.807355 | 1.945910 |
| 8 | 0.903090 | 3 | 2.079442 |
| 9 | 0.954243 | 3.169925 | 2.197225 |
| 10 | 1 | 3.321928 | 2.302585 |
| 20 | 1.301030 | 4.321928 | 2.995732 |
| 30 | 1.477121 | 4.906891 | 3.401197 |
| 40 | 1.602060 | 5.321928 | 3.688879 |
| 50 | 1.698970 | 5.643856 | 3.912023 |
| 60 | 1.778151 | 5.906991 | 4.094345 |
| 70 | 1.845098 | 6.129283 | 4.248495 |
| 80 | 1.903090 | 6.321928 | 4.382027 |
| 90 | 1.954243 | 6.491853 | 4.499810 |
| 100 | 2 | 6.643856 | 4.605170 |
| 200 | 2.301030 | 7.643856 | 5.298317 |
| 300 | 2.477121 | 8.228819 | 5.703782 |
| 400 | 2.602060 | 8.643856 | 5.991465 |
| 500 | 2.698970 | 8.965784 | 6.214608 |
| 600 | 2.778151 | 9.228819 | 6.396930 |
| 700 | 2.845098 | 9.451211 | 6.551080 |
| 800 | 2.903090 | 9.643856 | 6.684612 |
| 900 | 2.954243 | 9.813781 | 6.802395 |
| 1000 | 3 | 9.965784 | 6.907755 |
| 10000 | 4 | 13.287712 | 9.210340 |
Lihat juga
- Peraturan logaritma
- Perubahan asas logaritma
- Logaritma sifar
- Logaritma satu
- Logaritma tak terhingga
- Logaritma nombor negatif
- Kalkulator logaritma
- Graf logaritma
- Jadual logaritma
- Kalkulator logaritma semula jadi
- Logaritma semula jadi - ln x
- e pemalar
- Decibel (dB)