Kwadratische vergelijking
Kwadratische vergelijking is een polynoom van de tweede orde met 3 coëfficiënten - a , b , c .
De kwadratische vergelijking wordt gegeven door:
bijl 2 + bx + c = 0
De oplossing voor de kwadratische vergelijking wordt gegeven door 2 getallen x 1 en x 2 .
We kunnen de kwadratische vergelijking veranderen in de vorm van:
( x - x 1 ) ( x - x 2 ) = 0
Kwadratische formule
De oplossing voor de kwadratische vergelijking wordt gegeven door de kwadratische formule:
![]()
De uitdrukking binnen de vierkantswortel wordt discriminant genoemd en wordt aangeduid met Δ:
Δ = b 2 - 4 ac
De kwadratische formule met discriminante notatie:
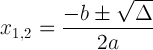
Deze uitdrukking is belangrijk omdat deze ons kan vertellen over de oplossing:
- Als Δ/ 0, zijn er 2 echte wortels x 1 = (- b + √ Δ ) / (2a) en x 2 = (- b-√ Δ ) / (2a) .
- Als Δ = 0, is er één wortel x 1 = x 2 = -b / (2a) .
- Als Δ <0, zijn er geen echte wortels, dan zijn er 2 complexe wortels:
x 1 = (- b + i√ -Δ ) / (2a) en x 2 = (- bi√ -Δ ) / (2a) .
Probleem # 1
3 x 2 +5 x +2 = 0
oplossing:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
Probleem # 2
3 x 2 -6 x 3 = 0
oplossing:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
Probleem # 3
x 2 +2 x +5 = 0
oplossing:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
Er zijn geen echte oplossingen. De waarden zijn complexe getallen:
X 1 = -1 + 2 ik
X 2 = -1 - 2 ik
Kwadratische functiegrafiek
De kwadratische functie is een polynoomfunctie van de tweede orde:
f ( x ) = bijl 2 + bx + c
De oplossingen voor de kwadratische vergelijking zijn de wortels van de kwadratische functie, dat wil zeggen de snijpunten van de kwadratische functiegrafiek met de x-as, wanneer
f ( x ) = 0
Als er 2 snijpunten zijn van de grafiek met de x-as, zijn er 2 oplossingen voor de kwadratische vergelijking.
Als er 1 snijpunt van de grafiek met de x-as is, is er 1 oplossing voor de kwadratische vergelijking.
Als er geen snijpunten van de grafiek met de x-as zijn, krijgen we geen echte oplossingen (of 2 complexe oplossingen).