Natuurlijke logaritme - ln (x)
Natuurlijke logaritme is de logaritme met de grondtal e van een getal.
- Natuurlijke logaritme (ln) definitie
- Regels en eigenschappen van natuurlijke logaritme (ln)
- Complexe logaritme
- Grafiek van ln (x)
- Natuurlijke logaritmen (ln) tabel
- Natuurlijke logaritme-calculator
Definitie van natuurlijke logaritme
Wanneer
e y = x
Dan is de logaritme van x met grondtal e
ln ( x ) = logboek e ( x ) = y
De constante e of het getal van Euler is:
e ≈ 2,71828183
Ln als inverse functie van exponentiële functie
De natuurlijke logaritmefunctie ln (x) is de inverse functie van de exponentiële functie e x .
Voor x/ 0,
f ( f -1 ( x )) = e ln ( x ) = x
Of
f -1 ( f ( x )) = ln ( e X ) = x
Regels en eigenschappen van natuurlijke logaritme
| Regelnaam | Regel | Voorbeeld |
|---|---|---|
Productregel |
ln ( x ∙ y ) = ln ( x ) + ln ( y ) |
ln (3 ∙ 7) = ln (3) + ln (7) |
Quotiënt regel |
ln ( x / y ) = ln ( x ) - ln ( y ) |
ln (3 / 7) = ln (3) - ln (7) |
Machtsregel |
ln ( x y ) = y ∙ ln ( x ) |
ln (2 8 ) = 8 ∙ ln (2) |
ln derivaat |
f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x | |
ln integraal |
∫ ln ( X ) dx = X ∙ (ln ( X ) - 1) + C | |
ln van negatief getal |
ln ( x ) is niet gedefinieerd wanneer x ≤ 0 | |
ln van nul |
ln (0) is niet gedefinieerd | |
ln van een |
ln (1) = 0 | |
ln van oneindigheid |
lim ln ( x ) = ∞, wanneer x → ∞ | |
| Euler's identiteit | ln (-1) = ik π |
Logaritme-productregel
De logaritme van de vermenigvuldiging van x en y is de som van logaritme van x en logaritme van y.
logboek b ( x ∙ y ) = logboek b ( x ) + logboek b ( y )
Bijvoorbeeld:
logboek 10 (3 ∙ 7) = logboek 10 (3) + logboek 10 (7)
Logaritme-quotiëntregel
De logaritme van de deling van x en y is het verschil van logaritme van x en logaritme van y.
logboek b ( x / y ) = logboek b ( x ) - logboek b ( y )
Bijvoorbeeld:
log 10 (3 / 7) = log 10 (3) - log 10 (7)
Logaritme machtsregel
De logaritme van x verheven tot de macht van y is y maal de logaritme van x.
logboek b ( x y ) = y ∙ logboek b ( x )
Bijvoorbeeld:
logboek 10 (2 8 ) = 8 ∙ logboek 10 (2)
Afgeleide van natuurlijke logaritme
De afgeleide van de natuurlijke logaritmefunctie is de reciproque functie.
Wanneer
f ( x ) = ln ( x )
De afgeleide van f (x) is:
f ' ( x ) = 1 / x
Integraal van natuurlijke logaritme
De integraal van de natuurlijke logaritmefunctie wordt gegeven door:
Wanneer
f ( x ) = ln ( x )
De integraal van f (x) is:
∫ f ( x ) dx = ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C
Ln van 0
De natuurlijke logaritme van nul is niet gedefinieerd:
ln (0) is niet gedefinieerd
De limiet nabij 0 van de natuurlijke logaritme van x, wanneer x nul nadert, is min oneindig:
![]()
Ln van 1
De natuurlijke logaritme van één is nul:
ln (1) = 0
Ln van oneindigheid
De limiet van de natuurlijke logaritme van oneindig, wanneer x oneindig nadert, is gelijk aan oneindig:
lim ln ( x ) = ∞, wanneer x → ∞
Complexe logaritme
Voor complex getal z:
z = re iθ = x + iy
De complexe logaritme is (n = ...- 2, -1,0,1,2, ...):
Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + Y 2 )) + i · arctan ( y / x ))
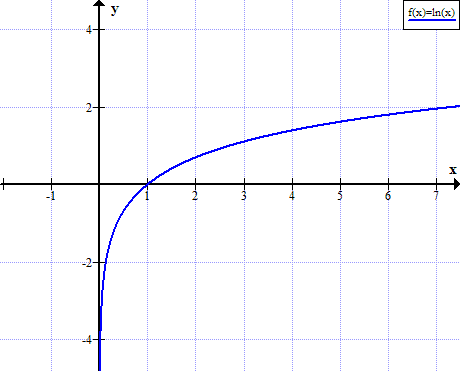
Grafiek van ln (x)
ln (x) is niet gedefinieerd voor echte niet-positieve waarden van x:
Tabel met natuurlijke logaritmen
| x | ln x |
|---|---|
| 0 | ongedefinieerd |
| 0 + | - ∞ |
| 0.0001 | -9.210340 |
| 0,001 | -6.907755 |
| 0,01 | -4.605170 |
| 0.1 | -2.302585 |
| 1 | 0 |
| 2 | 0,693147 |
| e ≈ 2,7183 | 1 |
| 3 | 1.098612 |
| 4 | 1.386294 |
| 5 | 1.609438 |
| 6 | 1.791759 |
| 7 | 1.945910 |
| 8 | 2.079442 |
| 9 | 2.197225 |
| 10 | 2.302585 |
| 20 | 2.995732 |
| 30 | 3.401197 |
| 40 | 3.688879 |
| 50 | 3.912023 |
| 60 | 4.094345 |
| 70 | 4.248495 |
| 80 | 4.382027 |
| 90 | 4.499810 |
| 100 | 4.605170 |
| 200 | 5.298317 |
| 300 | 5.703782 |
| 400 | 5,991465 |
| 500 | 6.214608 |
| 600 | 6.396930 |
| 700 | 6.551080 |
| 800 | 6.684612 |
| 900 | 6.802395 |
| 1000 | 6.907755 |
| 10000 | 9.210340 |
Zie ook
- Logaritme (logboek)
- Natuurlijke logaritme-calculator
- Natuurlijke logaritme van nul
- Natuurlijke logaritme van één
- Natuurlijke logaritme van e
- Natuurlijke logaritme van oneindigheid
- Natuurlijke logaritme van negatief getal
- Ln inverse functie
- ln (x) grafiek
- Natuurlijke logaritme-tabel
- Logaritme rekenmachine
- e constante
ALGEBRA
SNELLE TABELLEN