Variantie
In waarschijnlijkheid en statistiek is de variantie van een willekeurige variabele de gemiddelde waarde van de vierkante afstand tot de gemiddelde waarde. Het geeft weer hoe de willekeurige variabele wordt verdeeld in de buurt van de gemiddelde waarde. Kleine variantie geeft aan dat de willekeurige variabele dichtbij de gemiddelde waarde is verdeeld. Grote variantie geeft aan dat de willekeurige variabele ver van de gemiddelde waarde is verdeeld. Bij een normale verdeling zal de smalle belcurve bijvoorbeeld een kleine variantie hebben en een brede belcurve een grote variatie.
Variantie definitie
De variantie van willekeurige variabele X is de verwachte waarde van kwadraten van verschil van X en de verwachte waarde μ.
σ 2 = Var ( X ) = E [( X - μ ) 2 ]
Uit de definitie van de variantie die we kunnen halen
σ 2 = Var ( X ) = E ( X 2 ) - μ 2
Variantie van continue willekeurige variabele
Voor continue willekeurige variabele met gemiddelde waarde μ en kansdichtheidsfunctie f (x):
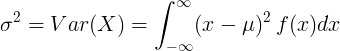
of
![Var (X) = \ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2](variance/cont_var2.gif)
Variantie van discrete willekeurige variabele
Voor discrete willekeurige variabele X met gemiddelde waarde μ en kansmassafunctie P (x):
![]()
of
![Var (X) = \ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right] - \ mu ^ 2](variance/disc_var2.gif)
Eigenschappen van variantie
Als X en Y onafhankelijke willekeurige variabelen zijn:
Var ( X + Y ) = Var ( X ) + Var ( Y )
Zie ook
WAARSCHIJNLIJKHEID & STATISTIEKEN
- Basiskans
- Verwachting
- Variantie
- Standaardafwijking
- Waarschijnlijkheidsverdeling
- Normale verdeling
- Statistieken symbolen
SNELLE TABELLEN