Kvadratisk ligning
Kvadratisk ligning er et andreordens polynom med 3 koeffisienter - a , b , c .
Den kvadratiske ligningen er gitt av:
øks 2 + bx + c = 0
Løsningen på den kvadratiske ligningen er gitt av 2 tall x 1 og x 2 .
Vi kan endre kvadratisk ligning til form av:
( x - x 1 ) ( x - x 2 ) = 0
Kvadratisk formel
Løsningen på den kvadratiske ligningen er gitt av den kvadratiske formelen:
![]()
Uttrykket inne i kvadratroten kalles diskriminerende og betegnes med Δ:
Δ = b 2 - 4 ac
Den kvadratiske formelen med diskriminerende notasjon:
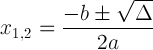
Dette uttrykket er viktig fordi det kan fortelle oss om løsningen:
- Når Δ/ 0 er det 2 reelle røtter x 1 = (- b + √ Δ ) / (2a) og x 2 = (- b-√ Δ ) / (2a) .
- Når Δ = 0, er det en rot x 1 = x 2 = -b / (2a) .
- Når Δ <0, er det ingen virkelige røtter, det er to komplekse røtter:
x 1 = (- b + i√ -Δ ) / (2a) og x 2 = (- bi√ -Δ ) / (2a) .
Problem nr. 1
3 x 2 +5 x +2 = 0
løsning:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
Oppgave 2
3 x 2 -6 x 3 = 0
løsning:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
Problem nr.3
x 2 +2 x +5 = 0
løsning:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
Det er ingen reelle løsninger. Verdiene er komplekse tall:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
Kvadratisk funksjonsgraf
Den kvadratiske funksjonen er en andre ordens polynomfunksjon:
f ( x ) = ax 2 + bx + c
Løsningene til den kvadratiske ligningen er røttene til den kvadratiske funksjonen, det vil si skjæringspunktene til den kvadratiske funksjonsgrafen med x-aksen, når
f ( x ) = 0
Når det er to skjæringspunkter i grafen med x-aksen, er det to løsninger på den kvadratiske ligningen.
Når det er ett skjæringspunkt på grafen med x-aksen, er det en løsning på den kvadratiske ligningen.
Når det ikke er noen skjæringspunkter i grafen med x-aksen, får vi ikke reelle løsninger (eller 2 komplekse løsninger).