Naturlig logaritme - ln (x)
Naturlig logaritme er logaritmen til basen e av et tall.
- Naturlig logaritme (ln) definisjon
- Natural logarithm (ln) regler og egenskaper
- Kompleks logaritme
- Graf av ln (x)
- Naturlige logaritmer (ln) tabell
- Naturlig logaritmekalkulator
Definisjon av naturlig logaritme
Når
e y = x
Da er basis e logaritmen til x
ln ( x ) = log e ( x ) = y
Den e konstant eller Eulers tall er:
e ≈ 2.71828183
Ln som invers funksjon av eksponensiell funksjon
Den naturlige logaritmefunksjonen ln (x) er den omvendte funksjonen til den eksponensielle funksjonen e x .
For x/ 0,
f ( f -1 ( x )) = e ln ( x ) = x
Eller
f -1 ( f ( x )) = ln ( e x ) = x
Naturlige logaritmeregler og egenskaper
| Regelnavn | Regel | Eksempel |
|---|---|---|
Produktregel |
ln ( x ∙ y ) = ln ( x ) + ln ( y ) |
ln (3 ∙ 7) = ln (3) + ln (7) |
Kvotientregel |
ln ( x / y ) = ln ( x ) - ln ( y ) |
ln (3 / 7) = ln (3) - ln (7) |
Maktregel |
ln ( x y ) = y ∙ ln ( x ) |
ln (2 8 ) = 8 ∙ ln (2) |
I derivat |
f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x | |
integrert |
∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C | |
ln negativt tall |
ln ( x ) er udefinert når x ≤ 0 | |
I null |
ln (0) er udefinert | |
I en |
ln (1) = 0 | |
I uendelig |
lim ln ( x ) = ∞, når x → ∞ | |
| Eulers identitet | ln (-1) = i π |
Logaritmeproduktregel
Logaritmen til multiplikasjonen av x og y er summen av logaritmen til x og logaritmen til y.
log b ( x ∙ y ) = log b ( x ) + log b ( y )
For eksempel:
logg 10 (3 ∙ 7) = logg 10 (3) + logg 10 (7)
Logaritmekvotientregel
Logaritmen til divisjonen av x og y er forskjellen på logaritmen til x og logaritmen til y.
log b ( x / y ) = log b ( x ) - log b ( y )
For eksempel:
log 10 (3 / 7) = log 10 (3) - log 10 (7)
Logaritmens maktregel
Logaritmen til x hevet til kraften til y er y ganger logaritmen til x.
log b ( x y ) = y ∙ log b ( x )
For eksempel:
logg 10 (2 8 ) = 8 ∙ logg 10 (2)
Derivat av naturlig logaritme
Derivatet av den naturlige logaritmefunksjonen er den gjensidige funksjonen.
Når
f ( x ) = ln ( x )
Derivatet av f (x) er:
f ' ( x ) = 1 / x
Integral av naturlig logaritme
Integralen av den naturlige logaritmefunksjonen er gitt av:
Når
f ( x ) = ln ( x )
Integralet av f (x) er:
∫ f ( x ) dx = ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C
Ln på 0
Den naturlige logaritmen til null er udefinert:
ln (0) er udefinert
Grensen nær 0 av den naturlige logaritmen til x, når x nærmer seg null, er minus uendelig:
![]()
Ln av 1
Den naturlige logaritmen til en er null:
ln (1) = 0
Ln av uendelig
Grensen for uendelig logaritme når x nærmer seg uendelig er lik uendelig:
lim ln ( x ) = ∞, når x → ∞
Kompleks logaritme
For kompleks nummer z:
z = re iθ = x + iy
Den komplekse logaritmen vil være (n = ...- 2, -1,0,1,2, ...):
Logg z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))
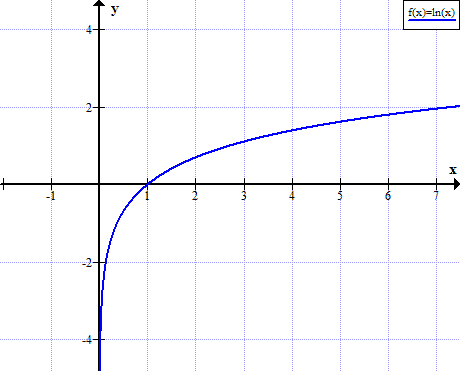
Graf av ln (x)
ln (x) er ikke definert for reelle ikke-positive verdier av x:
Naturlig logaritmisk tabell
| x | ln x |
|---|---|
| 0 | udefinert |
| 0 + | - ∞ |
| 0,0001 | -9.210340 |
| 0,001 | -6,907755 |
| 0,01 | -4,605170 |
| 0,1 | -2,302585 |
| 1 | 0 |
| 2 | 0,693147 |
| e ≈ 2.7183 | 1 |
| 3 | 1.098612 |
| 4 | 1.386294 |
| 5 | 1.609438 |
| 6 | 1.791759 |
| 7 | 1,945910 |
| 8 | 2.079442 |
| 9 | 2.197225 |
| 10 | 2.302585 |
| 20 | 2.995732 |
| 30 | 3.401197 |
| 40 | 3.688879 |
| 50 | 3.912023 |
| 60 | 4.094345 |
| 70 | 4.248495 |
| 80 | 4.382027 |
| 90 | 4.499810 |
| 100 | 4.605170 |
| 200 | 5.298317 |
| 300 | 5.703782 |
| 400 | 5.991465 |
| 500 | 6.214608 |
| 600 | 6.396930 |
| 700 | 6.551080 |
| 800 | 6,684612 |
| 900 | 6.802395 |
| 1000 | 6,907755 |
| 10000 | 9.210340 |
Se også
- Logaritme (logg)
- Naturlig logaritmekalkulator
- Naturlig logaritme på null
- Naturlig logaritme av en
- Naturlig logaritme av e
- Naturlig uendelig logaritme
- Naturlig logaritme med negativt tall
- Ln invers funksjon
- ln (x) graf
- Naturlig logaritmebord
- Logaritmekalkulator
- e konstant
ALGEBRA
RAPID BORD