Equação quadrática
A equação quadrática é um polinômio de segunda ordem com 3 coeficientes - a , b , c .
A equação quadrática é dada por:
machado 2 + bx + c = 0
A solução para a equação quadrática é dada por 2 números x 1 ex 2 .
Podemos mudar a equação quadrática para a forma de:
( x - x 1 ) ( x - x 2 ) = 0
Fórmula quadrática
A solução para a equação quadrática é dada pela fórmula quadrática:
![]()
A expressão dentro da raiz quadrada é chamada de discriminante e é denotada por Δ:
Δ = b 2 - 4 ac
A fórmula quadrática com notação discriminante:
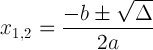
Esta expressão é importante porque pode nos dizer sobre a solução:
- Quando Δ/ 0, há 2 raízes reais x 1 = (- b + √ Δ ) / (2a) e x 2 = (- b-√ Δ ) / (2a) .
- Quando Δ = 0, há uma raiz x 1 = x 2 = -b / (2a) .
- Quando Δ <0, não há raízes reais, há 2 raízes complexas:
x 1 = (- b + i√ -Δ ) / (2a) e x 2 = (- bi√ -Δ ) / (2a) .
Problema # 1
3 x 2 +5 x +2 = 0
solução:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
Problema # 2
3 x 2 -6 x +3 = 0
solução:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
Problema # 3
x 2 +2 x +5 = 0
solução:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
Não existem soluções reais. Os valores são números complexos:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
Gráfico de Função Quadrática
A função quadrática é uma função polinomial de segunda ordem:
f ( x ) = ax 2 + bx + c
As soluções para a equação quadrática são as raízes da função quadrática, que são os pontos de intersecção do gráfico da função quadrática com o eixo x, quando
f ( x ) = 0
Quando há 2 pontos de interseção do gráfico com o eixo x, há 2 soluções para a equação quadrática.
Quando há 1 ponto de interseção do gráfico com o eixo x, há 1 solução para a equação quadrática.
Quando não há pontos de interseção do gráfico com o eixo x, não obtemos soluções reais (ou 2 soluções complexas).