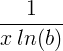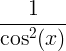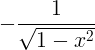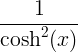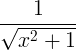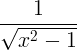Regras derivadas
Regras e leis derivadas. Tabela de derivadas de funções.
Definição derivada
A derivada de uma função é a razão da diferença do valor da função f (x) nos pontos x + Δx e x com Δx, quando Δx é infinitesimalmente pequeno. A derivada é a inclinação da função ou inclinação da reta tangente no ponto x.
![]()
Segunda derivada
A segunda derivada é dada por:
![]()
Ou simplesmente derive a primeira derivada:
![]()
Derivada enésima
A n- ésima derivada é calculada derivando f (x) n vezes.
A n- ésima derivada é igual à derivada da (n-1) derivada:
f ( n ) ( x ) = [ f ( n -1) ( x )] '
Exemplo:
Encontre a quarta derivada de
f ( x ) = 2 x 5
f (4) ( x ) = [2 x 5 ] '' '' = [10 x 4 ] '' '= [40 x 3 ]' '= [120 x 2 ]' = 240 x
Derivada no gráfico de função
A derivada de uma função é a inclinação da reta tangencial.
Regras derivadas
| Regra de soma derivada | ( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x ) |
| Regra de produto derivado | ( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x ) |
| Regra do quociente derivado | 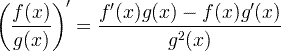 |
| Regra de cadeia derivada | f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x ) |
Regra de soma derivada
Quando a e b são constantes.
( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Exemplo:
Encontre a derivada de:
3 x 2 + 4 x.
De acordo com a regra da soma:
a = 3, b = 4
f ( x ) = x 2 , g ( x ) = x
f ' ( x ) = 2 x , g' ( x ) = 1
(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4
Regra de produto derivado
( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Regra do quociente derivado
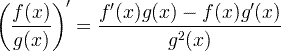
Regra de cadeia derivada
f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )
Esta regra pode ser melhor entendida com a notação de Lagrange:
![]()
Aproximação linear de função
Para Δx pequeno, podemos obter uma aproximação para f (x 0 + Δx), quando sabemos f (x 0 ) e f '(x 0 ):
f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) ⋅Δ x
Tabela de derivadas de funções
| Nome da função | Função | Derivado |
|---|---|---|
| f ( x ) |
f '( x ) | |
| Constante | const |
0 |
| Linear | x |
1 |
| Poder | x a |
machado a- 1 |
| Exponencial | e x |
e x |
| Exponencial | a x |
a x ln a |
| Logaritmo natural | ln ( x ) |
|
| Logaritmo | log b ( x ) |
|
| Seno | sin x |
cos x |
| Cosine | cos x |
-sin x |
| Tangente | tan x |
|
| Arcsine | arcsin x |
|
| Arccosine | arccos x |
|
| Arctangent | arctan x |
|
| Seno hiperbólico | sinh x |
cosh x |
| Cosseno hiperbólico | cosh x |
sinh x |
| Tangente hiperbólica | tanh x |
|
| Seno hiperbólico inverso | sinh -1 x |
|
| Cosseno hiperbólico inverso | cosh -1 x |
|
| Tangente hiperbólica inversa | tanh -1 x |
|
Exemplos derivados
Exemplo 1
f ( x ) = x 3 +5 x 2 + x +8
f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1
Exemplo # 2
f ( x ) = sin (3 x 2 )
Ao aplicar a regra da cadeia:
f ' ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]' = cos (3 x 2 ) ⋅ 6 x
Teste de segunda derivada
Quando a primeira derivada de uma função é zero no ponto x 0 .
f '( x 0 ) = 0
Então, a segunda derivada no ponto x 0 , f '' (x 0 ), pode indicar o tipo desse ponto:
| f '' ( x 0 )/ 0 |
mínimo local |
| f '' ( x 0 ) <0 |
máximo local |
| f '' ( x 0 ) = 0 |
indeterminado |
Veja também
CÁLCULO
- Limite
- Derivado
- Integrante
- Series
- Transformada de Laplace
- Convolução
- Símbolos de cálculo
TABELAS RÁPIDAS