Ecuația pătratică
Ecuația pătratică este un polinom de ordinul doi cu 3 coeficienți - a , b , c .
Ecuația pătratică este dată de:
ax 2 + bx + c = 0
Soluția la ecuația pătratică este dată de 2 numere x 1 și x 2 .
Putem schimba ecuația pătratică la forma:
( x - x 1 ) ( x - x 2 ) = 0
Formula quadratică
Soluția la ecuația pătratică este dată de formula pătratică:
![]()
Expresia din rădăcina pătrată se numește discriminantă și este notată cu Δ:
Δ = b 2 - 4 ac
Formula pătratică cu notație discriminantă:
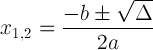
Această expresie este importantă, deoarece ne poate spune despre soluție:
- Când Δ/ 0, există 2 rădăcini reale x 1 = (- b + √ Δ ) / (2a) și x 2 = (- b-√ Δ ) / (2a) .
- Când Δ = 0, există o rădăcină x 1 = x 2 = -b / (2a) .
- Când Δ <0, nu există rădăcini reale, există 2 rădăcini complexe:
x 1 = (- b + i√ -Δ ) / (2a) și x 2 = (- bi√ -Δ ) / (2a) .
Problema nr. 1
3 x 2 +5 x +2 = 0
soluţie:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
Problema # 2
3 x 2 -6 x +3 = 0
soluţie:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
Problema # 3
x 2 +2 x +5 = 0
soluţie:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
Nu există soluții reale. Valorile sunt numere complexe:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
Grafic de funcții quadratic
Funcția pătratică este o funcție polinomială de ordinul doi:
f ( x ) = ax 2 + bx + c
Soluțiile la ecuația pătratică sunt rădăcinile funcției pătratice, adică punctele de intersecție ale graficului funcției pătratice cu axa x, când
f ( x ) = 0
Când există 2 puncte de intersecție ale graficului cu axa x, există 2 soluții la ecuația pătratică.
Când există 1 punct de intersecție al graficului cu axa x, există 1 soluție la ecuația pătratică.
Când nu există puncte de intersecție ale graficului cu axa x, nu obținem soluții reale (sau 2 soluții complexe).