Reguli de logaritm
De bază b logaritmul unui număr este exponentul de care avem nevoie pentru a ridica bază , în scopul de a obține numărul.
- Definiția logaritmului
- Reguli de logaritm
- Probleme de logaritm
- Logaritm complex
- Graficul jurnalului (x)
- Tabel logaritmic
- Calculator de logaritm
Definiția logaritmului
Când b este ridicat la puterea lui y este egal cu x:
b y = x
Apoi logaritmul bazei b al lui x este egal cu y:
log b ( x ) = y
De exemplu când:
2 4 = 16
Apoi
log 2 (16) = 4
Logaritmul ca funcție inversă a funcției exponențiale
Funcția logaritmică,
y = log b ( x )
este funcția inversă a funcției exponențiale,
x = b y
Deci, dacă calculăm funcția exponențială a logaritmului lui x (x/ 0),
f ( f -1 ( x )) = b log b ( x ) = x
Sau dacă calculăm logaritmul funcției exponențiale a lui x,
f -1 ( f ( x )) = log b ( b x ) = x
Logaritm natural (ln)
Logaritmul natural este un logaritm la baza e:
ln ( x ) = log e ( x )
Când e constantă este numărul:
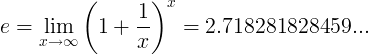
sau
![]()
Vezi: Logaritm natural
Calculul logaritmului invers
Logaritmul invers (sau anti logaritmul) este calculat prin ridicarea bazei b la logaritmul y:
x = log -1 ( y ) = b y
Funcția logaritmică
Funcția logaritmică are forma de bază a:
f ( x ) = log b ( x )
Reguli de logaritm
| Numele regulii | Regulă |
|---|---|
Regula produsului Logaritm |
log b ( x ∙ y ) = log b ( x ) + log b ( y ) |
Regula coeficientului logaritmului |
log b ( x / y ) = log b ( x ) - log b ( y ) |
Regula puterii logaritmice |
log b ( x y ) = y ∙ log b ( x ) |
Regula comutatorului de bază logaritmică |
log b ( c ) = 1 / log c ( b ) |
Regula de schimbare a bazei logaritmului |
log b ( x ) = log c ( x ) / log c ( b ) |
Derivată a logaritmului |
f ( x ) = log b ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( b )) |
Integrala logaritmului |
∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C |
Logaritmul numărului negativ |
jurnalul b ( x ) este nedefinit când x ≤ 0 |
Logaritmul lui 0 |
jurnalul b (0) este nedefinit |
Logaritmul lui 1 |
log b (1) = 0 |
Logaritmul bazei |
log b ( b ) = 1 |
Logaritmul infinitului |
lim log b ( x ) = ∞, când x → ∞ |
Vezi: Regulile logaritmului
Regula produsului Logaritm
Logaritmul înmulțirii lui x și y este suma logaritmului lui x și logaritmului lui y.
log b ( x ∙ y ) = log b ( x ) + log b ( y )
De exemplu:
log 10 (3 ∙ 7) = log 10 (3) + log 10 (7)
Regula coeficientului logaritmului
Logaritmul diviziunii lui x și y este diferența dintre logaritmul lui x și logaritmul lui y.
log b ( x / y ) = log b ( x ) - log b ( y )
De exemplu:
log 10 (3 / 7) = log 10 (3) - log 10 (7)
Regula puterii logaritmice
Logaritmul lui x ridicat la puterea lui y este de y ori logaritmul lui x.
log b ( x y ) = y ∙ log b ( x )
De exemplu:
log 10 (2 8 ) = 8 ∙ log 10 (2)
Regula comutatorului de bază logaritmică
Logaritmul bazei b al lui c este 1 împărțit la logaritmul bazei c al lui b.
log b ( c ) = 1 / log c ( b )
De exemplu:
jurnal 2 (8) = 1 / jurnal 8 (2)
Regula de schimbare a bazei logaritmului
Logaritmul bazei b al lui x este logaritmul bazei c al lui x împărțit la logaritmul bazei c al lui b.
log b ( x ) = log c ( x ) / log c ( b )
De exemplu, pentru a calcula jurnalul 2 (8) în calculator, trebuie să schimbăm baza la 10:
log 2 (8) = log 10 (8) / log 10 (2)
A se vedea: regula de modificare a bazei de jurnal
Logaritmul numărului negativ
Baza logaritmului real al lui x când x <= 0 este nedefinită când x este negativ sau egal cu zero:
jurnalul b ( x ) este nedefinit când x ≤ 0
A se vedea: jurnalul numărului negativ
Logaritmul lui 0
Logaritmul de bază b al zero este nedefinit:
jurnalul b (0) este nedefinit
Limita logaritmului de bază b al lui x, când x se apropie de zero, este minus infinit:
![]()
Vezi: jurnal de zero
Logaritmul lui 1
Logaritmul de bază b al unuia este zero:
log b (1) = 0
De exemplu, logaritmul bazei două a unuia este zero:
jurnal 2 (1) = 0
Vezi: jurnalul unuia
Logaritmul infinitului
Limita logaritmului de bază b al lui x, când x se apropie de infinit, este egală cu infinitul:
lim log b ( x ) = ∞, când x → ∞
Vezi: jurnalul infinitului
Logaritmul bazei
Logaritmul de bază b al lui b este unul:
log b ( b ) = 1
De exemplu, logaritmul de bază două a două este unul:
jurnal 2 (2) = 1
Derivat logaritmic
Cand
f ( x ) = log b ( x )
Apoi derivata lui f (x):
f ' ( x ) = 1 / ( x ln ( b ))
Vezi: derivat log
Integrală logaritmică
Integrala logaritmului lui x:
∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C
De exemplu:
∫ log 2 ( x ) dx = x ∙ (log 2 ( x ) - 1 / ln (2) ) + C
Aproximarea logaritmului
log 2 ( x ) ≈ n + ( x / 2 n - 1),
Logaritm complex
Pentru numărul complex z:
z = re iθ = x + iy
Logaritmul complex va fi (n = ...- 2, -1,0,1,2, ...):
Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))
Probleme și răspunsuri de logaritm
Problema nr. 1
Găsiți x pentru
log 2 ( x ) + log 2 ( x -3) = 2
Soluţie:
Utilizarea regulii produsului:
log 2 ( x ∙ ( x -3)) = 2
Schimbarea formei logaritmului în conformitate cu definiția logaritmului:
x ∙ ( x -3) = 2 2
Sau
x 2 -3 x -4 = 0
Rezolvarea ecuației pătratice:
x 1,2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4, -1
Deoarece logaritmul nu este definit pentru numerele negative, răspunsul este:
x = 4
Problema # 2
Găsiți x pentru
log 3 ( x +2) - log 3 ( x ) = 2
Soluţie:
Folosind regula coeficientului:
log 3 (( x +2) / x ) = 2
Schimbarea formei logaritmului în conformitate cu definiția logaritmului:
( x +2) / x = 3 2
Sau
x +2 = 9 x
Sau
8 x = 2
Sau
x = 0,25
Graficul jurnalului (x)
log (x) nu este definit pentru valorile reale pozitive ale lui x:
Tabel de logaritmi
| x | jurnal 10 x | jurnal 2 x | log e x |
|---|---|---|---|
| 0 | nedefinit | nedefinit | nedefinit |
| 0 + | - ∞ | - ∞ | - ∞ |
| 0,0001 | -4 | -13.287712 | -9.210340 |
| 0,001 | -3 | -9.965784 | -6.907755 |
| 0,01 | -2 | -6.643856 | -4.605170 |
| 0,1 | -1 | -3.321928 | -2.302585 |
| 1 | 0 | 0 | 0 |
| 2 | 0,301030 | 1 | 0,693147 |
| 3 | 0,471212 | 1.584963 | 1.098612 |
| 4 | 0,602060 | 2 | 1.386294 |
| 5 | 0,698970 | 2.321928 | 1.609438 |
| 6 | 0,778151 | 2.584963 | 1.791759 |
| 7 | 0,845098 | 2.807355 | 1.945910 |
| 8 | 0,903090 | 3 | 2.079442 |
| 9 | 0,954243 | 3.169925 | 2.197225 |
| 10 | 1 | 3.321928 | 2.302585 |
| 20 | 1.301030 | 4.321928 | 2.995732 |
| 30 | 1.477121 | 4.906891 | 3.401197 |
| 40 | 1.602060 | 5.321928 | 3.688879 |
| 50 | 1.698970 | 5.643856 | 3.912023 |
| 60 | 1.778151 | 5.906991 | 4.094345 |
| 70 | 1.845098 | 6.129283 | 4.248495 |
| 80 | 1.903090 | 6.321928 | 4.382027 |
| 90 | 1.954243 | 6.491853 | 4.499810 |
| 100 | 2 | 6.643856 | 4.605170 |
| 200 | 2.301030 | 7.643856 | 5.298317 |
| 300 | 2.477121 | 8.228819 | 5.703782 |
| 400 | 2.602060 | 8.643856 | 5,991465 |
| 500 | 2.698970 | 8.965784 | 6.214608 |
| 600 | 2.778151 | 9.228819 | 6.396930 |
| 700 | 2,845098 | 9.451211 | 6.551080 |
| 800 | 2.903090 | 9.643856 | 6.684612 |
| 900 | 2.954243 | 9.813781 | 6,802395 |
| 1000 | 3 | 9.965784 | 6.907755 |
| 10000 | 4 | 13.287712 | 9.210340 |
Vezi si
- Reguli de logaritm
- Schimbarea logaritmului de bază
- Logaritmul zero
- Logaritmul unuia
- Logaritmul infinitului
- Logaritmul numărului negativ
- Calculator de logaritm
- Grafic logaritmic
- Tabel logaritmic
- Calculator de logaritm natural
- Logaritm natural - ln x
- e constantă
- Decibel (dB)
