Varianța

În probabilitate și statistici, varianța unei variabile aleatorii este valoarea medie a distanței pătrate față de valoarea medie. Reprezintă modul în care variabila aleatoare este distribuită lângă valoarea medie. Varianța mică indică faptul că variabila aleatorie este distribuită în apropierea valorii medii. Varianța mare indică faptul că variabila aleatorie este distribuită departe de valoarea medie. De exemplu, cu distribuție normală, curba clopotului îngust va avea o varianță mică, iar curba clopotului larg va avea o varianță mare.

Definiția varianței

Varianța variabilei aleatorii X este valoarea așteptată a pătratelor de diferență de X și valoarea așteptată μ.

σ ² = Var ( X ) = E [( X - μ ) ² ]

Din definiția varianței putem obține

σ ² = Var ( X ) = E ( X ² ) - μ ²

Varianța variabilei aleatoare continue

Pentru variabila aleatorie continuă cu valoarea medie μ și funcția densității probabilității f (x):

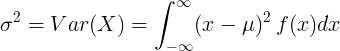
$\ sigma ^ 2 = Var (X) = \ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx$

$Var (X) = \ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2$

Variația variabilei discrete aleatorii

Pentru variabila discretă aleatoare X cu valoarea medie μ și funcția de masă de probabilitate P (x):

$\ sigma ^ 2 = Var (X) = \ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)$

$Var (X) = \ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right] - \ mu ^ 2$

Proprietățile varianței

Când X și Y sunt variabile aleatoare independente:

Var ( X + Y ) = Var ( X ) + Var ( Y )

Abaterea standard ►

Varianța

Definiția varianței

Varianța variabilei aleatoare continue

Variația variabilei discrete aleatorii

Proprietățile varianței

Var ( X + Y ) = Var ( X ) + Var ( Y )

Vezi si

PROBABILITATE ȘI STATISTICĂ

MESE RAPIDE