Konvolucija
Konvolucija je korelacijska funkcija f (τ) z obrnjeno funkcijo g (t-τ).
Operator konvolucije je simbol zvezdice * .
- Neprekinjeno zvijanje
- Diskretna konvolucija
- 2D diskretna konvolucija
- Filtrirajte izvedbo s konvolucijo
- Teorem o konvoluciji
Neprekinjeno zvijanje
Konvolacija f (t) in g (t) je enaka integralu f (τ) krat f (t-τ):
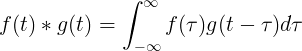
Diskretna konvolucija
Konvolucija dveh ločenih funkcij je definirana kot:
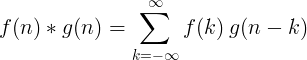
2D diskretna konvolucija
Za obdelavo slik se običajno uporablja dvodimenzionalna diskretna konvolucija.
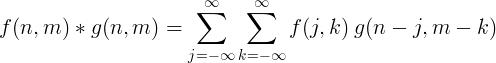
Filtrirajte izvedbo s konvolucijo
Diskretni vhodni signal x (n) lahko filtriramo s konvolucijo z impulznim odzivom h (n), da dobimo izhodni signal y (n).
y ( n ) = x ( n ) * h ( n )
Teorem o konvoluciji
Fourierjeva transformacija množenja 2 funkcij je enaka konvoluciji Fourierjevih transformacij vsake funkcije:
ℱ { f ⋅ g } = ℱ { f } * ℱ { g }
Fourierjeva transformacija konvolucije dveh funkcij je enaka množenju Fourierjevih transformacij vsake funkcije:
ℱ { f * g } = ℱ { f } ℱ ℱ { g }
Konvolucijski izrek za kontinuirano Fourierjevo transformacijo
ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )
ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )
Konvolucijski izrek za diskretno Fourierjevo transformacijo
ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )
ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )
Teorem o konvoluciji za Laplaceovo transformacijo
ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )
Poglej tudi
KALKUL
- Omejitev
- Izvedeni finančni instrumenti
- Celovito
- Serije
- Laplasova transformacija
- Konvolucija
- Simboli računa
HITRE MIZE