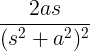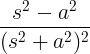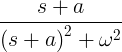Laplaceova preobrazba
- Laplasova funkcija pretvorbe
- Tabela Laplaceove transformacije
- Lastnosti Laplaceove transformacije
- Primeri Laplaceove transformacije
Laplaceova transformacija pretvori funkcijo časovne domene v funkcijo s-domene z integracijo od nič do neskončnosti
funkcije časovne domene, pomnoženo z e -st .
Laplaceova transformacija se uporablja za hitro iskanje rešitev za diferencialne enačbe in integrale.
Izpeljava v časovni domeni se v s-domeni pretvori v množenje s s.
Integracija v časovni domeni se spremeni v delitev s v s-domeni.
Laplasova funkcija pretvorbe
Laplasova transformacija je definirana z operatorjem L {}:
![]()
Inverzna Laplasova transformacija
Inverzno Laplasovo transformacijo lahko izračunamo neposredno.
Običajno je inverzna transformacija podana iz tabele transformacij.
Tabela Laplaceove transformacije
| Ime funkcije | Funkcija časovne domene | Laplasova transformacija |
|---|---|---|
f ( t ) |
F ( s ) = L { f ( t )} |
|
| Stalno | 1 | |
| Linearno | t | |
| Moč | t n |
|
| Moč | t a |
Γ ( 1) ⋅ y - ( 1) |
| Eksponent | e na |
|
| Sinus | greh pri |
|
| Cosine | cos at |
|
| Hiperbolični sinus | sinh at |
|
| Hiperbolični kosinus | cosh pri |
|
| Gojenje sinusa | t sin na |
|
| Gojenje kosinusa | t cos at |
|
| Razpadajoči sinus | e -at sin ωt |
|
| Propadajoči kosinus | e -at cos ωt |
|
| Delta funkcija | δ ( t ) |
1 |
| Zakasnjena delta | δ ( ta ) |
e -as |
Lastnosti Laplaceove transformacije
| Ime lastnosti | Funkcija časovne domene | Laplasova transformacija | Komentiraj |
|---|---|---|---|
f ( t ) |
F ( s ) |
||
| Linearnost | af ( t ) + bg ( t ) | aF ( s ) + bG ( s ) | a , b so konstantne |
| Sprememba lestvice | f ( pri ) | |
a / 0 |
| Shift | e -at f ( t ) | F ( s + a ) | |
| Zamuda | f ( ta ) | e - kot F ( s ) | |
| Izpeljava | |
sF ( s ) - f (0) | |
| N-ta izpeljava | |
s n f ( s ) - s n -1 f (0) - s n -2 f '(0) -...- f ( n -1) (0) | |
| Moč | t n f ( t ) | |
|
| Integracija | |
|
|
| Vzajemno | |
|
|
| Konvolucija | f ( t ) * g ( t ) | F ( s ) ⋅ G ( s ) | * je operater konvolucije |
| Periodična funkcija | f ( t ) = f ( t + T ) | |
Primeri Laplaceove transformacije
Primer # 1
Poiščite pretvorbo f (t):
f ( t ) = 3 t + 2 t 2
Rešitev:
ℒ { t } = 1 / s 2
ℒ { t 2 } = 2 / s 3
F ( s ) = ℒ { f ( t )} = ℒ {3 t + 2 t 2 } = 3ℒ { t } + 2ℒ { t 2 } = 3 / s 2 + 4 / s 3
2. primer
Poiščite obratno transformacijo F (s):
F ( s ) = 3 / ( s 2 + s - 6)
Rešitev:
Da bi našli obratno transformacijo, moramo funkcijo domene s spremeniti v preprostejšo obliko:
F ( s ) = 3 / ( s 2 + s - 6) = 3 / [( s -2) ( s +3)] = a / ( s -2) + b / ( s +3)
[ a ( s +3) + b ( s -2)] / [( s -2) ( s +3)] = 3 / [( s -2) ( s +3)]
a ( s +3) + b ( s -2) = 3
Da najdemo a in b, dobimo 2 enačbi - eno od s koeficientov in drugo od preostalih:
( a + b ) s + 3 a -2 b = 3
a + b = 0, 3 a -2 b = 3
a = 3/5, b = -3/5
F ( s ) = 3/5 ( s -2) - 3/5 ( s +3)
Zdaj lahko F (s) enostavno pretvorite z uporabo tabele pretvorb za eksponentno funkcijo:
f ( t ) = (3/5) e 2 t - (3/5) e -3 t
Poglej tudi
KALKUL
- Omejitev
- Izvedeni finančni instrumenti
- Celovito
- Serije
- Laplasova transformacija
- Konvolucija
- Simboli računa
HITRE MIZE