Porazdelitev verjetnosti
V verjetnosti in statistiki je porazdelitev značilnost naključne spremenljivke, ki opisuje verjetnost naključne spremenljivke v vsaki vrednosti.
Vsaka porazdelitev ima določeno funkcijo gostote verjetnosti in funkcijo porazdelitve verjetnosti.
Čeprav obstaja verjetnostno neomejeno število porazdelitev, je v uporabi več običajnih porazdelitev.
Kumulativna funkcija porazdelitve
Porazdelitev verjetnosti je opisana s kumulativno funkcijo porazdelitve F (x),
kar je verjetnost, da bo naključna spremenljivka X dobila vrednost, manjšo ali enako x:
F ( x ) = P ( X ≤ x )
Neprekinjena distribucija
Kumulativna funkcija porazdelitve F (x) se izračuna z integracijo funkcije gostote verjetnosti f (u) zvezne naključne spremenljivke X.
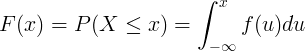
Diskretna porazdelitev
Kumulativna funkcija porazdelitve F (x) se izračuna s seštevanjem funkcije verjetnosti mase P (u) diskretne naključne spremenljivke X.
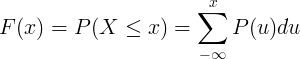
Tabela neprekinjenih distribucij
Neprekinjena porazdelitev je porazdelitev zvezne naključne spremenljivke.
Primer stalne distribucije
...
Tabela neprekinjenih distribucij
| Ime distribucije | Simbol za distribucijo | Funkcija gostote verjetnosti (pdf) | Pomeni | Varianca |
|---|---|---|---|---|
| f X ( x ) |
μ = E ( X ) |
σ 2 = Var ( X ) |
||
| Običajno / gaussian | X ~ N (μ, σ 2 ) |
|
μ | σ 2 |
| Enotna | X ~ U ( a , b ) |
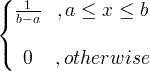 |
|
|
| Eksponentno | X ~ exp (λ) | |
|
|
| Gama | X ~ gama ( c , λ) | 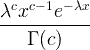 x / 0, c / 0, λ/ 0 |
|
|
| Chi kvadrat | X ~ χ 2 ( k ) |
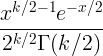 |
k |
2 k |
| Wishart | ||||
| F | X ~ F ( k 1 , k 2 ) |
|||
| Beta | ||||
| Weibull | ||||
| Dnevnik normalno | X ~ LN (μ, σ 2 ) |
|||
| Rayleigh | ||||
| Cauchy | ||||
| Dirichlet | ||||
| Laplace | ||||
| Levy | ||||
| Riž | ||||
| Študentska t |
Tabela diskretnih porazdelitev
Diskretna porazdelitev je porazdelitev diskretne naključne spremenljivke.
Primer diskretne distribucije
...
Tabela diskretnih porazdelitev
| Ime distribucije | Simbol za distribucijo | Funkcija verjetnosti mase (pmf) | Pomeni | Varianca | |
|---|---|---|---|---|---|
| f x ( k ) = P ( X = k ) k = 0,1,2, ... |
E ( x ) | Var ( x ) | |||
| Binomna | X ~ koš ( n , p ) |
|
np |
np (1- str ) |
|
| Poisson | X ~ Poisson (λ) |
|
λ ≥ 0 |
λ |
λ |
| Enotna | X ~ U ( a, b ) |
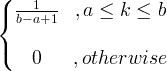 |
|
|
|
| Geometrijska | X ~ Geom ( p ) |
|
|
|
|
| Hiper-geometrijska | X ~ HG ( N , K , n ) |
 |
N = 0,1,2, ... K = 0,1, .., N n = 0,1, ..., N |
|
|
| Bernoulli | X ~ Bern ( p ) |
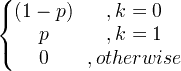 |
p |
p (1- p ) |
|
Poglej tudi
VERJETNOST IN STATISTIKA
- Osnovna verjetnost
- Pričakovanje
- Varianca
- Standardni odklon
- Porazdelitev verjetnosti
- Običajna porazdelitev
- Statistični simboli
HITRE MIZE