Standardni odklon

V verjetnosti in statistiki je standardni odklon naključne spremenljivke povprečna oddaljenost naključne spremenljivke od srednje vrednosti.

Predstavlja, kako se naključna spremenljivka porazdeli blizu srednje vrednosti. Majhen standardni odklon kaže, da je naključna spremenljivka porazdeljena blizu srednje vrednosti. Velik standardni odklon kaže, da je naključna spremenljivka porazdeljena daleč od srednje vrednosti.

Formula definicije standardnega odklona

Standardni odklon je kvadratni koren variance naključne spremenljivke X s srednjo vrednostjo μ.

\ sigma = std (X) = \ sqrt {Var (X)} = \ sqrt {E ((X- \ mu) ^ 2}

Iz opredelitve standardnega odklona lahko dobimo

\ sigma = std (X) = \ sqrt {E (X ^ 2) - \ mu ^ 2}

Standardni odklon zvezne naključne spremenljivke

Za zvezno naključno spremenljivko s srednjo vrednostjo μ in funkcijo gostote verjetnosti f (x):

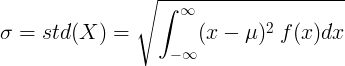
\ sigma = std (X) = \ sqrt {\ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx}

ali

\ sigma = std (X) = \ sqrt {\ levo [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ desno] - \ mu ^ 2}

Standardni odklon diskretne naključne spremenljivke

Za diskretno naključno spremenljivko X s srednjo vrednostjo μ in verjetnostno masno funkcijo P (x):

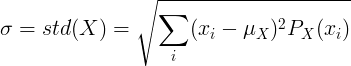
\ sigma = std (X) = \ sqrt {\ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)}

ali

\ sigma = std (X) = \ sqrt {\ levo [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ desno] - \ mu ^ 2}

 

Porazdelitev verjetnosti ►

 

Poglej tudi

VERJETNOST IN STATISTIKA
HITRE MIZE