Kvadratisk ekvation
Kvadratisk ekvation är en andra ordningens polynom med 3 koefficienter - a , b , c .
Kvadratiska ekvationen ges av:
ax 2 + bx + c = 0
Lösningen på den kvadratiska ekvationen ges av 2 siffror x 1 och x 2 .
Vi kan ändra den kvadratiske ekvationen till formen av:
( x - x 1 ) ( x - x 2 ) = 0
Kvadratiska formel
Lösningen på den kvadratiska ekvationen ges med den kvadratiska formeln:
![]()
Uttrycket inuti kvadratroten kallas diskriminerande och betecknas med Δ:
A = b 2 - 4 ac
Kvadratformeln med diskriminerande notation:
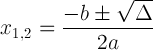
Detta uttryck är viktigt eftersom det kan berätta om lösningen:
- När Δ/ 0 finns det 2 verkliga rötter x 1 = (- b + √ Δ ) / (2a) och x 2 = (- b-√ Δ ) / (2a) .
- När Δ = 0 finns en rot x 1 = x 2 = -b / (2a) .
- När Δ <0 finns det inga verkliga rötter, det finns två komplexa rötter:
x 1 = (- b + i√ -Δ ) / (2a) och x 2 = (- bi√ -Δ ) / (2a) .
Problem nr 1
3 x 2 +5 x +2 = 0
lösning:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
Problem nr 2
3 x 2 -6 x 3 = 0
lösning:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
Problem nr 3
x 2 +2 x +5 = 0
lösning:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
Det finns inga riktiga lösningar. Värdena är komplexa tal:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
Kvadratisk funktionsgraf
Den kvadratiska funktionen är en andra ordningens polynomfunktion:
f ( x ) = ax 2 + bx + c
Lösningarna på den kvadratiska ekvationen är rötterna till den kvadratiska funktionen, det vill säga skärningspunkterna för den kvadratiska funktionsdiagrammet med x-axeln, när
f ( x ) = 0
När det finns två skärningspunkter i diagrammet med x-axeln finns det två lösningar på den kvadratiska ekvationen.
När det finns en skärningspunkt i diagrammet med x-axeln finns det en lösning på den kvadratiska ekvationen.
När det inte finns några skärningspunkter i diagrammet med x-axeln får vi inte riktiga lösningar (eller två komplexa lösningar).