Naturlig logaritm - ln (x)

Naturlig logaritm är logaritmen till basen av ett tal.

Definition av naturlig logaritm

När

e y = x

Då är bas e-logaritmen för x

ln ( x ) = log e ( x ) = y

 

Den e konstant eller Eulers nummer är:

e ≈ 2.71828183

Ln som invers funktion av exponentiell funktion

Den naturliga logaritmfunktionen ln (x) är den inversa funktionen hos den exponentiella funktionen e x .

För x/ 0,

f ( f -1 ( x )) = e ln ( x ) = x

Eller

f -1 ( f ( x )) = ln ( e x ) = x

Naturliga logaritmregler och egenskaper

Regelnamn Regel Exempel
Produktregel

ln ( x ∙ y ) = ln ( x ) + ln ( y )

ln (3 ∙ 7) = ln (3) + ln (7)
Kvotientregel

ln ( x / y ) = ln ( x ) - ln ( y )

ln (3 / 7) = ln (3) - ln (7)
Kraftregel

ln ( x y ) = y ∙ ln ( x )

ln (2 8 ) = 8 ∙ ln (2)
I derivat
 f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x  
en integrerad
 ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C  
ln av negativt tal
 ln ( x ) är odefinierad när x ≤ 0  
noll
 ln (0) är odefinierad  
 
av en
 ln (1) = 0  
av oändligheten
 lim ln ( x ) = ∞, när x → ∞  
Eulers identitet ln (-1) = i π  

 

Logaritmproduktregel

Logaritmen för multiplikationen av x och y är summan av logaritmen för x och logaritmen för y.

log b ( x ∙ y ) = log b ( x ) + log b ( y )

Till exempel:

logg 10 (3 ∙ 7) = logg 10 (3) + logg 10 (7)

Logaritmkvotientregel

Logaritmen för delningen av x och y är skillnaden mellan logaritmen för x och logaritmen för y.

log b ( x / y ) = log b ( x ) - log b ( y )

Till exempel:

log 10 (3 / 7) = log 10 (3) - log 10 (7)

Logaritmens kraftregel

Logaritmen för x höjd till y-effekten är y gånger logaritmen för x.

log b ( x y ) = y ∙ log b ( x )

Till exempel:

logg 10 (2 8 ) = 8 ∙ logg 10 (2)

Derivat av naturlig logaritm

Derivat av den naturliga logaritmfunktionen är den ömsesidiga funktionen.

När

f ( x ) = ln ( x )

Derivatet av f (x) är:

f ' ( x ) = 1 / x

Integral av naturlig logaritm

Integralen i den naturliga logaritmfunktionen ges av:

När

f ( x ) = ln ( x )

Integralen av f (x) är:

∫ f ( x ) dx = ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C

Ln av 0

Den naturliga logaritmen om noll är odefinierad:

ln (0) är odefinierad

Gränsen nära 0 för den naturliga logaritmen av x, när x närmar sig noll, är minus oändlighet:

Ln av 1

Den naturliga logaritmen för en är noll:

ln (1) = 0

Ln av oändligheten

Gränsen för oändlighetens naturliga logaritm när x närmar sig oändligheten är lika med oändligheten:

lim ln ( x ) = ∞, när x → ∞

Komplex logaritm

För komplexa nummer z:

z = re iθ = x + iy

Den komplexa logaritmen kommer att vara (n = ...- 2, -1,0,1,2, ...):

Logga z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))

Graf för ln (x)

ln (x) definieras inte för verkliga icke-positiva värden på x:

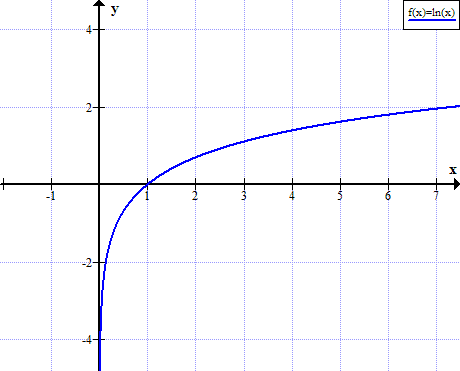
Naturlig logaritmtabell

x ln x
0 odefinierad
0 + - ∞
0,0001 -9.210340
0,001 -6,907755
0,01 -4.605170
0,1 -2,302585
1 0
2 0,693147
e ≈ 2.7183 1
3 1.098612
4 1.386294
5 1,609438
6 1.791759
7 1,945910
8 2,079442
9 2.197225
10 2.302585
20 2.995732
30 3.401197
40 3.688879
50 3.912023
60 4.094345
70 4.248495
80 4.382027
90 4.499810
100 4,605170
200 5.298317
300 5.703782
400 5,991465
500 6.214608
600 6.396930
700 6.551080
800 6,684612
900 6,802395
1000 6,907755
10000 9.210340

 

Logaritmregler ►

 

Se även

ALGEBRA
SNABBBORD