Logaritmregler

Den bas B logaritmen av ett antal är exponent att vi måste höja basen för att få numret.

Logaritmedefinition

När b höjs till effekten av y är lika med x:

b y = x

Då är basb logaritmen för x lika med y:

log b ( x ) = y

Till exempel när:

2 4 = 16

Sedan

log 2 (16) = 4

Logaritm som invers funktion av exponentiell funktion

Den logaritmiska funktionen,

y = log b ( x )

är den inversa funktionen hos den exponentiella funktionen,

x = b y

Så om vi beräknar den exponentiella funktionen för logaritmen av x (x/ 0),

f ( f -1 ( x )) = b log b ( x ) = x

Eller om vi beräknar logaritmen för den exponentiella funktionen av x,

f -1 ( f ( x )) = log b ( b x ) = x

Naturlig logaritm (ln)

Naturlig logaritm är en logaritm till basen e:

ln ( x ) = log e ( x )

När e-konstanten är antalet:

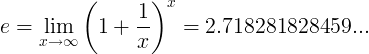
e = \ lim_ {x \ rightarrow \ infty} \ left (1+ \ frac {1} {x} \ right) ^ x = 2.718281828459 ...

eller

e = \ lim_ {x \ rightarrow 0} \ left (1+ \ right x) ^ \ frac {1} {x}

 

Se: Naturlig logaritm

Invers logaritmberäkning

Den inversa logaritmen (eller antilogaritmen) beräknas genom att höja basen b till logaritmen y:

x = log -1 ( y ) = b y

Logaritmisk funktion

Den logaritmiska funktionen har den grundläggande formen av:

f ( x ) = log b ( x )

Logaritmregler

Regelnamn Regel
Logaritmproduktregel
 log b ( x ∙ y ) = log b ( x ) + log b ( y )
Logaritmkvotientregel
 log b ( x / y ) = log b ( x ) - log b ( y )
Logaritmens kraftregel
 log b ( x y ) = y ∙ log b ( x )
Logaritm-basomkopplarregel
 log b ( c ) = 1 / log c ( b )
Logaritmbasändringsregel
 log b ( x ) = log c ( x ) / log c ( b )
Derivat av logaritm
 f ( x ) = log b ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( b ))
Integral av logaritmen
 ∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C
Logaritm med negativt tal
 log b ( x ) är odefinierad när x ≤ 0
Logaritm på 0
 log b (0) är odefinierad
\ lim_ {x \ till 0 ^ +} \ textup {log} _b (x) = - \ infty
Logaritm av 1
 log b (1) = 0
Logaritm av basen
 log b ( b ) = 1
Oändlighetens logaritm
 lim log b ( x ) = ∞, när x → ∞

Se: Logaritmregler

 

Logaritmproduktregel

Logaritmen för multiplikationen av x och y är summan av logaritmen för x och logaritmen för y.

log b ( x ∙ y ) = log b ( x ) + log b ( y )

Till exempel:

logg 10 (3 ∙ 7) = logg 10 (3) + logg 10 (7)

Logaritmkvotientregel

Logaritmen för delningen av x och y är skillnaden mellan logaritmen för x och logaritmen för y.

log b ( x / y ) = log b ( x ) - log b ( y )

Till exempel:

log 10 (3 / 7) = log 10 (3) - log 10 (7)

Logaritmens kraftregel

Logaritmen för x höjd till y-effekten är y gånger logaritmen för x.

log b ( x y ) = y ∙ log b ( x )

Till exempel:

logg 10 (2 8 ) = 8 ∙ logg 10 (2)

Logaritm-basomkopplarregel

Basen b logaritmen av c är 1 dividerad med basen c logaritmen av b.

log b ( c ) = 1 / log c ( b )

Till exempel:

log 2 (8) = 1 / log 8 (2)

Logaritmbasändringsregel

Bas b logaritmen av x är bas c logaritmen av x dividerat med basen c logaritmen av b.

log b ( x ) = log c ( x ) / log c ( b )

För att till exempel beräkna log 2 (8) i miniräknare måste vi ändra basen till 10:

log 2 (8) = log 10 (8) / log 10 (2)

Se: Ändra regel för logbas

Logaritm med negativt tal

Basen b reell logaritm av x när x <= 0 är odefinierad när x är negativ eller lika med noll:

log b ( x ) är odefinierad när x ≤ 0

Se: logg med negativt tal

Logaritm på 0

Bas-logaritmen på noll är odefinierad:

log b (0) är odefinierad

Gränsen för bas b-logaritmen för x, när x närmar sig noll, är minus oändlighet:

\ lim_ {x \ till 0 ^ +} \ textup {log} _b (x) = - \ infty

Se: log of zero

Logaritm av 1

Bas-logaritmen för en är noll:

log b (1) = 0

Till exempel är bas två logaritmer av en noll:

log 2 (1) = 0

Se: logg över en

Oändlighetens logaritm

Gränsen för basb logaritmen för x, när x närmar sig oändligheten, är lika med oändligheten:

lim log b ( x ) = ∞, när x → ∞

Se: log of infinity

Logaritm av basen

Bas b logaritmen för b är en:

log b ( b ) = 1

Till exempel är bas två logaritmen av två en:

log 2 (2) = 1

Logaritmderivat

När

f ( x ) = log b ( x )

Därefter derivatet av f (x):

f ' ( x ) = 1 / ( x ln ( b ))

Se: loggderivat

Logaritm integral

Integralen av logaritmen av x:

∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C

Till exempel:

∫ log 2 ( x ) dx = x ∙ (log 2 ( x ) - 1 / ln (2) ) + C

Logaritm approximation

log 2 ( x ) ≈ n + ( x / 2 n - 1),

Komplex logaritm

För komplexa nummer z:

z = re iθ = x + iy

Den komplexa logaritmen kommer att vara (n = ...- 2, -1,0,1,2, ...):

Logga z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))

Logaritmproblem och svar

Problem nr 1

Hitta x för

log 2 ( x ) + log 2 ( x -3) = 2

Lösning:

Använda produktregeln:

log 2 ( x ∙ ( x -3)) = 2

Ändra logaritmform enligt logaritmedefinitionen:

x ∙ ( x -3) = 2 2

Eller

x 2 -3 x -4 = 0

Lösa kvadratisk ekvation:

x 1,2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4, -1

Eftersom logaritmen inte är definierad för negativa tal är svaret:

x = 4

Problem nr 2

Hitta x för

log 3 ( x +2) - log 3 ( x ) = 2

Lösning:

Med kvotregeln:

logg 3 (( x +2) / x ) = 2

Ändra logaritmform enligt logaritmedefinitionen:

( x +2) / x = 3 2

Eller

x +2 = 9 x

Eller

8 x = 2

Eller

x = 0,25

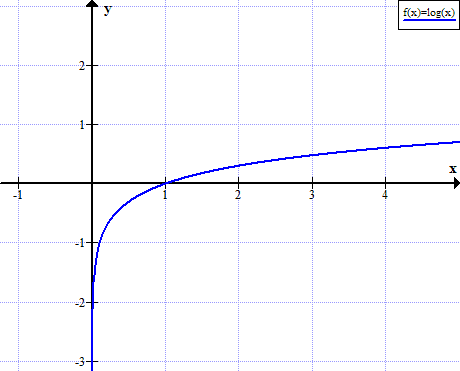
Graf för logg (x)

log (x) definieras inte för verkliga icke-positiva värden på x:

Logaritmtabell

x logga 10 x logga 2 x logga e x
0 odefinierad odefinierad odefinierad
0 + - ∞ - ∞ - ∞
0,0001 -4 -13,287712 -9.210340
0,001 -3 -9,965784 -6,907755
0,01 -2 -6,643856 -4.605170
0,1 -1 -3,321928 -2,302585
1 0 0 0
2 0,301030 1 0,693147
3 0.477121 1.584963 1.098612
4 0,602060 2 1.386294
5 0,698970 2.321928 1,609438
6 0,778151 2,584963 1.791759
7 0,845098 2.807355 1,945910
8 0,903090 3 2,079442
9 0,954243 3.169925 2.197225
10 1 3.321928 2.302585
20 1.301030 4.321928 2.995732
30 1.477121 4,906891 3.401197
40 1,602060 5.321928 3.688879
50 1.698970 5,643856 3.912023
60 1,778151 5,906991 4.094345
70 1,845098 6.129283 4.248495
80 1,903090 6.321928 4.382027
90 1,954243 6.491853 4.499810
100 2 6,643856 4,605170
200 2.301030 7,643856 5.298317
300 2.477121 8.228819 5.703782
400 2.602060 8.643856 5,991465
500 2.698970 8,965784 6.214608
600 2.778151 9.228819 6.396930
700 2.845098 9.451211 6.551080
800 2.903090 9,643856 6,684612
900 2,954243 9.813781 6,802395
1000 3 9,965784 6,907755
10000 4 13.287712 9.210340

 

Logaritmräknare ►

 

Se även

ALGEBRA
SNABBBORD