Nollnummer (0)
Definition av nollnummer
Noll är ett tal som används i matematik för att beskriva ingen kvantitet eller ingen kvantitet.
När det finns två äpplen på bordet och vi tar de två äpplen kan vi säga att det finns noll äpplen på bordet.
Nollnumret är inte positivt och inte negativt tal.
Nollan är också en siffra för platshållare i andra siffror (t.ex. 40.103, 170).
Är noll ett tal?
Noll är ett tal. Det är inte positivt eller negativt.
Noll siffra
Nollsiffran används som platshållare när du skriver siffror.
Till exempel:
204 = 2 × 100 + 0 × 10 + 4 × 1
Nollnummerhistorik
Vem uppfann nollnummer?
Den moderna 0-symbolen uppfanns i Indien på 600-talet och användes senare av perserna och araberna och senare i Europa.
Symbol för noll
Nollnumret betecknas med 0- symbolen.
Det arabiska siffersystemet använder symbolen ٠.
Nollnummeregenskaper
x representerar valfritt tal.
| Drift | Regel | Exempel |
|---|---|---|
Tillägg |
x + 0 = x |
3 + 0 = 3 |
Subtraktion |
x - 0 = x |
3 - 0 = 3 |
Multiplikation |
x × 0 = 0 |
5 × 0 = 0 |
Division |
0 ÷ x = 0 , när x ≠ 0 |
0 ÷ 5 = 0 |
| x ÷ 0 är odefinierad |
5 ÷ 0 är odefinierad |
|
Exponentiering |
0 x = 0 |
0 5 = 0 |
| x 0 = 1 |
5 0 = 1 |
|
Rot |
√ 0 = 0 |
|
Logaritm |
log b (0) är odefinierad |
|
| |
||
Faktor |
0! = 1 |
|
Sinus |
sin 0º = 0 |
|
Cosinus |
cos 0º = 1 |
|
Tangent |
solbränd 0º = 0 |
|
Derivat |
0 '= 0 |
|
Väsentlig |
∫ 0 d x = 0 + C. |
|
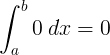 |
Noll tillägg
Tillägg av ett tal plus noll är lika med antalet:
x + 0 = x
Till exempel:
5 + 0 = 5
Noll subtraktion
Subtraktion av ett tal minus noll är lika med antalet:
x - 0 = x
Till exempel:
5 - 0 = 5
Multiplikation med noll
Multiplikation av ett antal gånger noll är lika med noll:
x × 0 = 0
Till exempel:
5 × 0 = 0
Nummer dividerat med noll
Delning av ett tal med noll definieras inte:
x ÷ 0 är odefinierad
Till exempel:
5 ÷ 0 är odefinierad
Noll dividerat med ett tal
Division av noll med ett tal är noll:
0 ÷ x = 0
Till exempel:
0 ÷ 5 = 0
Antal till nolleffekt
Kraften hos ett tal som höjs med noll är en:
x 0 = 1
Till exempel:
5 0 = 1
Logaritmen är noll
Bas-logaritmen på noll är odefinierad:
log b (0) är odefinierad
Det finns inget nummer vi kan höja basen b med för att få noll.
Endast gränsen för basb-logaritmen på x, när x konvergerar noll är minus oändlighet:
![]()
Uppsättningar som innehåller noll
Noll är ett element av de naturliga tal, heltal, reella tal och komplexa taluppsättningar:
| Ställ in | Ställ in medlemsnotation |
|---|---|
| Naturliga tal (ej negativa) | 0 ∈ ℕ 0 |
| Heltalsnummer | 0 ∈ ℤ |
| Riktiga nummer | 0 ∈ ℝ |
| Komplexa tal | 0 ∈ ℂ |
| Rationella nummer | 0 ∈ ℚ |
Är noll jämnt eller udda tal?
Uppsättningen med jämna siffror är:
{..., -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ...}
Uppsättningen med udda siffror är:
{..., -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, ...}
Noll är en heltalsmultipel av 2:
0 × 2 = 0
Noll är medlem i det jämna antalet:
0 ∈ {2 k , k ∈ℤ}
Så noll är ett jämnt tal och inte ett udda tal.
Är noll ett naturligt tal?
Det finns två definitioner för de naturliga siffrorna.
Uppsättningen av icke-negativa heltal:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Uppsättningen av positiva heltal:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Noll är medlem i uppsättningen icke-negativa heltal:
0 ∈ ℕ 0
Noll är inte medlem i uppsättningen positiva heltal:
0 ∉ ℕ 1
Är noll ett heltal?
Det finns tre definitioner för heltal:
Uppsättningen av heltal:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Uppsättningen av icke-negativa heltal:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Uppsättningen av positiva heltal:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Noll är medlem i uppsättningen heltal och uppsättningen icke-negativa heltal:
0 ∈ ℤ
0 ∈ ℕ 0
Noll är inte medlem i uppsättningen positiva heltal:
0 ∉ ℕ 1
Är noll ett heltal?
Uppsättningen av heltal:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Noll är medlem i uppsättningen heltal:
0 ∈ ℤ
Så noll är ett heltal.
Är noll ett rationellt tal?
Ett rationellt tal är ett tal som kan uttryckas som kvoten för två heltal:
ℚ = { n / m ; n , m ∈ℤ}
Noll kan skrivas som en kvot av två heltal.
Till exempel:
0 = 0/3
Så noll är ett rationellt tal.
Är noll ett positivt tal?
Ett positivt tal definieras som ett tal som är större än noll:
x / 0
Till exempel:
5/ 0
Eftersom noll inte är större än noll är det inte ett positivt tal.
Är noll ett primtal?
Siffran 0 är inte ett primtal.
Noll är inte ett positivt tal och har ett oändligt antal delare.
Det lägsta primtalet är 2.