సమగ్ర

ఏకీకరణ అనేది ఉత్పన్నం యొక్క రివర్స్ ఆపరేషన్.

ఫంక్షన్ యొక్క సమగ్ర ఫంక్షన్ యొక్క గ్రాఫ్ క్రింద ఉన్న ప్రాంతం.

నిరవధిక సమగ్ర నిర్వచనం

ఎప్పుడు dF (x) / dx = f (x) =/ సమగ్ర (f (x) * dx) = F (x) + c

నిరవధిక సమగ్ర లక్షణాలు

సమగ్ర (f (x) + g (x)) * dx = సమగ్ర (f (x) * dx) + సమగ్ర (g (x) * dx)

సమగ్ర (a * f (x) * dx) = a * సమగ్ర (f (x) * dx)

సమగ్ర (f (a * x) * dx) = 1 / a * F (a * x) + c

సమగ్ర (f (x + b) * dx) = F (x + b) + c

సమగ్ర (f (a * x + b) * dx) = 1 / a * F (a * x + b) + c

సమగ్ర (df (x) / dx * dx) = f (x)

ఇంటిగ్రేషన్ వేరియబుల్ యొక్క మార్పు

ఎప్పుడుx = g (t) మరియుdx = g '(t) * dt

సమగ్ర (f (x) * dx) = సమగ్ర (f (g (t)) * g '(t) * dt)

భాగాల వారీగా అనుసంధానం

సమగ్ర (f (x) * g '(x) * dx) = f (x) * g (x) - సమగ్ర (f' (x) * g (x) * dx)

ఇంటిగ్రల్స్ టేబుల్

సమగ్ర (f (x) * dx = F (x) + సి

సమగ్ర (a * dx) = a * x + c

సమగ్ర (x ^ n * dx) = 1 / (a ​​+ 1) * x ^ (a + 1) + c, ఉన్నప్పుడు </ - 1

సమగ్ర (1 / x * dx) = ln (abs (x)) + c

సమగ్ర (e ^ x * dx) = e ^ x + c

సమగ్ర (a ^ x * dx) = a ^ x / ln (x) + c

సమగ్ర (ln (x) * dx) = x * ln (x) - x + c

సమగ్ర (పాపం (x) * dx) = -కోస్ (x) + సి

సమగ్ర (cos (x) * dx) = పాపం (x) + సి

సమగ్ర (తాన్ (x) * dx) = -ln (abs (cos (x))) + c

సమగ్ర (ఆర్క్సిన్ (x) * dx) = x * ఆర్క్సిన్ (x) + చదరపు (1-x ^ 2) + సి

సమగ్ర (ఆర్కోస్ (x) * dx) = x * ఆర్కోస్ (x) - చదరపు (1-x ^ 2) + సి

సమగ్ర (ఆర్క్టాన్ (x) * dx) = x * ఆర్క్టాన్ (x) - 1/2 * ln (1 + x ^ 2) + సి

సమగ్ర (dx / (గొడ్డలి + బి)) = 1 / a * ln (abs (a * x + b)) + c

సమగ్ర (1 / sqrt (a ^ 2-x ^ 2) * dx) = arcsin (x / a) + c

సమగ్ర (1 / sqrt (x ^ 2 + - a ^ 2) * dx) = ln (abs (x + sqrt (x ^ 2 + - a ^ 2)) + c

సమగ్ర (x * sqrt (x ^ 2-a ^ 2) * dx) = 1 / (a ​​* arccos (x / a)) + c

సమగ్ర (1 / (a ​​^ 2 + x ^ 2) * dx) = 1 / a * arctan (x / a) + c

సమగ్ర (1 / (a ​​^ 2-x ^ 2) * dx) = 1/2a * ln (abs ((a + x) / (గొడ్డలి)) + c

సమగ్ర (సిన్హ్ (x) * dx) = కోష్ (x) + సి

సమగ్ర (cosh (x) * dx) = sinh (x) + c

సమగ్ర (tanh (x) * dx) = ln (cosh (x)) + c

 

ఖచ్చితమైన సమగ్ర నిర్వచనం

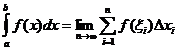
సమగ్ర (a..b, f (x) * dx) = lim (n-/ inf, sum (i = 1..n, f (z (i)) * dx (i))) 

ఎప్పుడుx0 = a, xn = b

dx (k) = x (k) - x (k-1)

x (k-1) <= z (k) <= x (k)

ఖచ్చితమైన సమగ్ర గణన

ఎప్పుడు ,

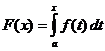 dF (x) / dx = f (x) మరియు

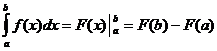
సమగ్ర (a..b, f (x) * dx) = F (b) - F (a) 

ఖచ్చితమైన సమగ్ర లక్షణాలు

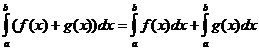
సమగ్ర (a..b, (f (x) + g (x)) * dx) = సమగ్ర (a..b, f (x) * dx) + సమగ్ర (a..b, g (x) * dx )

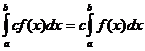
సమగ్ర (a..b, c * f (x) * dx) = c * సమగ్ర (a..b, f (x) * dx)

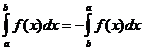
సమగ్ర (a..b, f (x) * dx) = - సమగ్ర (b..a, f (x) * dx)

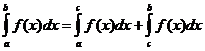
సమగ్ర (a..b, f (x) * dx) = సమగ్ర (a..c, f (x) * dx) + సమగ్ర (c..b, f (x) * dx)

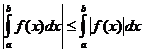
abs (సమగ్ర (a..b, f (x) * dx)) <= సమగ్ర (a..b, abs (f (x)) * dx)

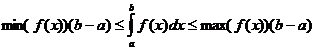min (f (x)) * (ba) <= సమగ్ర (a..b, f (x) * dx) <= గరిష్టంగా (f (x)) * (ba) ఎప్పుడు[a, b] యొక్క x సభ్యుడు

ఇంటిగ్రేషన్ వేరియబుల్ యొక్క మార్పు

ఎప్పుడుx = g (t) ,dx = g '(t) * dt ,g (ఆల్ఫా) = a ,g (బీటా) = బి

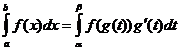
సమగ్ర (a..b, f (x) * dx) = సమగ్ర (ఆల్ఫా..బెటా, f (g (t)) * g '(t) * dt)

భాగాల వారీగా అనుసంధానం

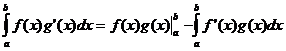
సమగ్ర (a..b, f (x) * g '(x) * dx) = సమగ్ర (a..b, f (x) * g (x) * dx) - సమగ్ర (a..b, f' (x) * g (x) * dx)

సగటు విలువ సిద్ధాంతం

చేసినప్పుడు f ( x ) నిరంతర ఒక పాయింట్ ఉందిc [a, b] లో సభ్యుడు కాబట్టి

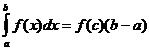
సమగ్ర (a..b, f (x) * dx) = f (c) * (ba)  

ట్రాపెజాయిడల్ డెఫినిట్ ఇంటిగ్రల్ యొక్క ఉజ్జాయింపు

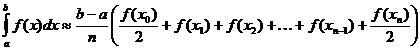
సమగ్ర (a..b, f (x) * dx) ~ (ba) / n * (f (x (0)) / 2 + f (x (1)) + f (x (2)) + .. . + f (x (n-1)) + f (x (n)) / 2)

గామా ఫంక్షన్

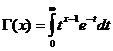
గామా (x) = సమగ్ర (0..ఇన్ఫ్, టి ^ (x-1) * ఇ ^ (- టి) * డిటి

గామా ఫంక్షన్ x/ 0 కోసం కన్వర్జెంట్ .

గామా ఫంక్షన్ గుణాలు

G ( x +1) = x G ( x )

G ( n +1) = n ! , ఉన్నప్పుడు n ℕ (పాజిటివ్ పూర్ణాంకం).సభ్యుడు

బీటా ఫంక్షన్

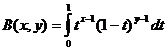
B (x, y) = సమగ్ర (0..1, t ^ (n-1) * (1-t) ^ (y-1) * dt

బీటా ఫంక్షన్ మరియు గామా ఫంక్షన్ సంబంధం

బి (x, y) = గామా (x) * గామా (y) / గామా (x + y)

 

 

 

కాలిక్యులస్
రాపిడ్ టేబుల్స్