การแปลง

การแปลงเป็นฟังก์ชันสหสัมพันธ์ของ f (τ) กับฟังก์ชันย้อนกลับ g (t-τ)

ผู้ประกอบการบิดเป็นสัญลักษณ์เครื่องหมายดอกจัน*

การรวมกันของ f (t) และ g (t) เท่ากับอินทิกรัลของ f (τ) คูณ f (t-τ):

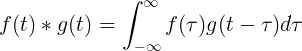
$f (t) * g (t) = \ int _ {- \ infty} ^ {\ infty} f (\ tau) g (t- \ tau) d \ tau$

การแปลงของฟังก์ชันแยก 2 ฟังก์ชันถูกกำหนดให้เป็น:

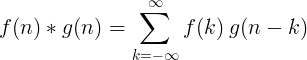
$f (n) * g (n) = \ sum_ {k = - \ infty} ^ {\ infty} f (k) \: g (nk)$

โดยปกติจะใช้คอนโวลูชันแบบแยก 2 มิติสำหรับการประมวลผลภาพ

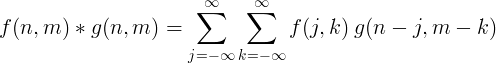
$f (n, m) * g (n, m) = \ sum_ {j = - \ infty} ^ {\ infty} \ sum_ {k = - \ infty} ^ {\ infty} f (j, k) \: กรัม (nj, mk)$

เราสามารถกรองสัญญาณอินพุตแบบไม่ต่อเนื่อง x (n) โดยการแปลงสัญญาณด้วยการตอบสนองอิมพัลส์ h (n) เพื่อรับสัญญาณเอาต์พุต y (n)

y ( n ) = x ( n ) * h ( n )

การแปลงฟูเรียร์ของการคูณของ 2 ฟังก์ชันเท่ากับการแปลงของการแปลงฟูริเยร์ของแต่ละฟังก์ชัน:

ℱ { f ⋅ g } = ℱ { f } * ℱ { g }

การแปลงฟูเรียร์ของคอนโวลูชั่นของ 2 ฟังก์ชันเท่ากับการคูณของการแปลงฟูเรียร์ของแต่ละฟังก์ชัน:

ℱ { f * g } = ℱ { f } ⋅ℱ { g }

ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )

ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )

ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )

ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ℱ { g ( n )} = F ( k ) ⋅ G ( k )

ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ℒ { g ( t )} = F ( s ) ⋅ G ( s )

ดูสิ่งนี้ด้วย