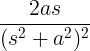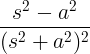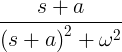Laplace Transform
Laplace transform แปลงฟังก์ชันโดเมนเวลาเป็นฟังก์ชัน s-domain โดยการรวมจากศูนย์ถึงอินฟินิตี้
การทำงานของโดเมนเวลาคูณด้วยอี -st
การแปลงลาปลาซใช้เพื่อค้นหาคำตอบสำหรับสมการเชิงอนุพันธ์และปริพันธ์อย่างรวดเร็ว
การหาที่มาในโดเมนเวลาจะถูกเปลี่ยนเป็นการคูณด้วย s ในโดเมน s
การรวมในโดเมนเวลาถูกเปลี่ยนเป็นการหารด้วย s ใน s-domain
ฟังก์ชั่นการแปลง Laplace
การแปลง Laplace ถูกกำหนดด้วยตัวดำเนินการL {}:
![]()
การแปลง Laplace ผกผัน
สามารถคำนวณการแปลง Laplace ผกผันได้โดยตรง
โดยปกติการแปลงผกผันจะได้รับจากตารางการแปลง
โต๊ะแปลงร่าง Laplace
| ชื่อฟังก์ชัน | ฟังก์ชันโดเมนเวลา | ลาปลาซแปลงร่าง |
|---|---|---|
ฉ ( t ) |
F ( s ) = L { f ( t )} |
|
| คงที่ | 1 | |
| เชิงเส้น | t | |
| อำนาจ | เสื้อn |
|
| อำนาจ | เสื้อก |
Γ ( a +1) ⋅ s - ( a +1) |
| เลขชี้กำลัง | e ที่ |
|
| ไซน์ | บาปที่ |
|
| โคไซน์ | cos ที่ |
|
| ไฮเพอร์โบลิกไซน์ | บาปที่ |
|
| ไฮเพอร์โบลิกโคไซน์ | cosh ที่ |
|
| ไซน์ที่กำลังเติบโต | tบาปที่ |
|
| การปลูกโคไซน์ | t cos ที่ |
|
| ไซน์ที่สลายตัว | e- at sin ωt |
|
| โคไซน์ที่สลายตัว | e- at cos ωt |
|
| ฟังก์ชันเดลต้า | δ ( เสื้อ ) |
1 |
| เดลต้าล่าช้า | δ ( TA ) |
e -as |
คุณสมบัติการแปลง Laplace
| ชื่อคุณสมบัติ | ฟังก์ชันโดเมนเวลา | ลาปลาซแปลงร่าง | แสดงความคิดเห็น |
|---|---|---|---|
ฉ ( t ) |
F ( s ) |
||
| ความเป็นเส้นตรง | af ( เสื้อ ) + bg ( t ) | AF ( s ) + BG ( s ) | a , bเป็นค่าคงที่ |
| การเปลี่ยนแปลงขนาด | f ( ที่ ) | |
a / 0 |
| กะ | e - ที่ f ( t ) | F ( s + a ) | |
| ล่าช้า | f ( ตา ) | e - เป็น F ( s ) | |
| ที่มา | |
sF ( s ) - ฉ (0) | |
| อนุพันธ์ N-th | |
s n f ( s ) - s n -1 f (0) - s n -2 f '(0) -...- f ( n -1) (0) | |
| อำนาจ | เสื้อn f ( เสื้อ ) | |
|
| บูรณาการ | |
|
|
| ซึ่งกันและกัน | |
|
|
| การแปลง | f ( เสื้อ ) * g ( t ) | F ( s ) ⋅ G ( s ) | * เป็นตัวดำเนินการ Convolution |
| ฟังก์ชันเป็นระยะ | f ( เสื้อ ) = f ( t + T ) | |
ตัวอย่างการแปลง Laplace
ตัวอย่าง # 1
ค้นหาการเปลี่ยนแปลงของ f (t):
f ( t ) = 3 t + 2 t 2
วิธีการแก้:
ℒ { t } = 1 / s 2
ℒ { t 2 } = 2 / s 3
F ( s ) = ℒ { f ( t )} = ℒ {3 t + 2 t 2 } = 3ℒ { t } + 2ℒ { t 2 } = 3 / s 2 + 4 / s 3
ตัวอย่าง # 2
ค้นหาการแปลงผกผันของ F:
F ( s ) = 3 / ( s 2 + s - 6)
วิธีการแก้:
ในการค้นหาการแปลงผกผันเราจำเป็นต้องเปลี่ยนฟังก์ชัน s domain เป็นรูปแบบที่ง่ายกว่า:
F ( s ) = 3 / ( s 2 + s - 6) = 3 / [( s -2) ( s +3)] = a / ( s -2) + b / ( s +3)
[ a ( s +3) + b ( s -2)] / [( s -2) ( s +3)] = 3 / [( s -2) ( s +3)]
a ( s +3) + b ( s -2) = 3
ในการหา a และ b เราจะได้ 2 สมการ - หนึ่งในสัมประสิทธิ์ s และที่สองของส่วนที่เหลือ:
( a + b ) s + 3 a -2 b = 3
a + b = 0, 3 ก -2 b = 3
a = 3/5, b = -3/5
F ( s ) = 3/5 ( s -2) - 3/5 ( s +3)
ตอนนี้ F สามารถเปลี่ยนได้อย่างง่ายดายโดยใช้ตารางการแปลงสำหรับฟังก์ชันเลขชี้กำลัง:
f ( t ) = (3/5) จ2 t - (3/5) จ-3 t
ดูสิ่งนี้ด้วย
แคลคูลัส
- ขีด จำกัด
- อนุพันธ์
- อินทิกรัล
- ชุด
- ลาปลาซแปลงร่าง
- การแปลง
- สัญลักษณ์แคลคูลัส
ตารางอย่างรวดเร็ว