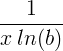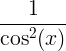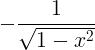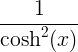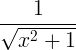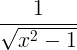กฎอนุพันธ์

กฎและกฎหมายอนุพันธ์ ตารางอนุพันธ์ของฟังก์ชัน

นิยามอนุพันธ์

อนุพันธ์ของฟังก์ชันคืออัตราส่วนของความแตกต่างของค่าฟังก์ชัน f (x) ที่จุด x + Δxและ x โดยมีΔxเมื่อΔxมีขนาดเล็กเพียงเล็กน้อย อนุพันธ์คือความชันของฟังก์ชันหรือความชันของเส้นสัมผัสที่จุด x

 

f '(x) = \ lim _ {\ Delta x \ ถึง 0} \ frac {f (x + \ Delta x) -f (x)} {\ Delta x}

อนุพันธ์อันดับสอง

อนุพันธ์อันดับสองกำหนดโดย:

หรือเพียงแค่ได้รับอนุพันธ์แรก:

ฉ '' (x) = (f '(x))'

อนุพันธ์ Nth

n TH อนุพันธ์คำนวณโดย deriving f (x) n ครั้ง

n TH อนุพันธ์เท่ากับที่มาของ (n-1) ตราสารอนุพันธ์:

f ( n ) ( x ) = [ f ( n -1) ( x )] '

ตัวอย่าง:

หาอนุพันธ์อันดับสี่ของ

f ( x ) = 2 x 5

f (4) ( x ) = [2 x 5 ] '' '' = [10 x 4 ] '' '= [40 x 3 ]' '= [120 x 2 ]' = 240 x

อนุพันธ์ของกราฟของฟังก์ชัน

อนุพันธ์ของฟังก์ชันคือสล็อปของเส้นสัมผัส

กฎอนุพันธ์

กฎผลรวมอนุพันธ์

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
กฎผลิตภัณฑ์อนุพันธ์

( f ( x ) ∙ ก ( x )) '= f' ( x ) ก ( x ) + f ( x ) ก ' ( x )
กฎผลหารอนุพันธ์ 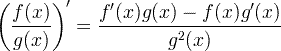\ left (\ frac {f (x)} {g (x)} \ right) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( x)}
กฎลูกโซ่อนุพันธ์

ฉ ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

กฎผลรวมอนุพันธ์

เมื่อaและbเป็นค่าคงที่

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )

ตัวอย่าง:

ค้นหาอนุพันธ์ของ:

3 x 2 + 4 x.

ตามกฎผลรวม:

a = 3, b = 4

f ( x ) = x 2 , ก ( x ) = x

f ' ( x ) = 2 x , ก' ( x ) = 1

(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

กฎผลิตภัณฑ์อนุพันธ์

( f ( x ) ∙ ก ( x )) '= f' ( x ) ก ( x ) + f ( x ) ก ' ( x )

กฎผลหารอนุพันธ์

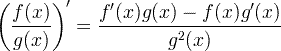
\ left (\ frac {f (x)} {g (x)} \ right) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( x)}

กฎลูกโซ่อนุพันธ์

ฉ ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

กฎนี้สามารถเข้าใจได้ดีขึ้นด้วยสัญกรณ์ของ Lagrange:

\ frac {df} {dx} = \ frac {df} {dg} \ cdot \ frac {dg} {dx}

ฟังก์ชันการประมาณเชิงเส้น

สำหรับΔxเล็กเราจะได้ค่าประมาณเป็น f (x 0 + Δx) เมื่อเรารู้ f (x 0 ) และ f '(x 0 ):

f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) ⋅Δ x

ตารางอนุพันธ์ของฟังก์ชัน

ชื่อฟังก์ชัน ฟังก์ชัน อนุพันธ์

f ( x )

 f '( x )
คงที่

const

0

เชิงเส้น

x

1

อำนาจ

x ก

ขวานก- 1
เอกซ์โปเนนเชียล

จx

จx
เอกซ์โปเนนเชียล

กx

กx ln ก
ลอการิทึมธรรมชาติ

ln ( x )

ลอการิทึม

บันทึกb ( x )

ไซน์

บาปx

cos x
โคไซน์

cos x

- ซินx
สัมผัส

ผิวสีแทนx

Arcsine

arcsin x

Arccosine

arccos x

อาร์กแทนเจนต์

อาร์กแทนx
ไฮเพอร์โบลิกไซน์

บาปx

cosh x
ไฮเพอร์โบลิกโคไซน์

cosh x

บาปx
ไฮเพอร์โบลิกแทนเจนต์

tanh x

ไฮเพอร์โบลิกไซน์ผกผัน

บาป-1 x

ไฮเพอร์โบลิกโคไซน์ผกผัน

cosh -1 x

แทนเจนต์ไฮเพอร์โบลิกผกผัน

tanh -1 x

ตัวอย่างอนุพันธ์

ตัวอย่าง # 1

f ( x ) = x 3 +5 x 2 + x +8

f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1

ตัวอย่าง # 2

f ( x ) = บาป (3 x 2 )

เมื่อใช้กฎลูกโซ่:

f ' ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]' = cos (3 x 2 ) ⋅ 6 x

การทดสอบอนุพันธ์ครั้งที่สอง

เมื่ออนุพันธ์แรกของฟังก์ชั่นเป็นศูนย์ที่จุด x 0

f '( x 0 ) = 0

จากนั้นอนุพันธ์อันดับสองที่จุด x 0 , f '' (x 0 ) สามารถระบุประเภทของจุดนั้น:

 

f '' ( x 0 )/ 0

 ขั้นต่ำในท้องถิ่น

f '' ( x 0 ) <0

 สูงสุดในท้องถิ่น

f '' ( x 0 ) = 0

 บึกบึน

 

ดูสิ่งนี้ด้วย

แคลคูลัส
ตารางอย่างรวดเร็ว