Conbolusyon

Ang Convolution ay ang pagpapaandar ng f (τ) na may pabaliktad na pagpapaandar g (t-τ).

Ang convolution operator ay ang simbolo ng asterisk * .

Patuloy na pag-unlad
Discrete convolution
2D discrete convolution
I-filter ang pagpapatupad sa convolution
Teoryang Convolusyon

Patuloy na pag-unlad

Ang convolution ng f (t) at g (t) ay katumbas ng integral ng f (τ) beses f (t-τ):

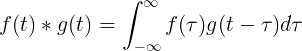
$f (t) * g (t) = \ int _ {- \ infty} ^ {\ infty} f (\ tau) g (t \ tau) d \ tau$

Discrete convolution

Ang pag-unlad ng 2 discrete function ay tinukoy bilang:

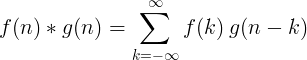
$f (n) * g (n) = \ sum_ {k = - \ infty} ^ {\ infty} f (k) \: g (nk)$

2D discrete convolution

Karaniwang ginagamit ang 2 dimensional na discrete convolution para sa pagproseso ng imahe.

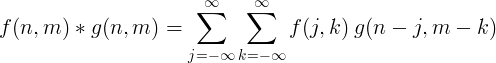
$f (n, m) * g (n, m) = \ sum_ {j = - \ infty} ^ {\ infty} \ sum_ {k = - \ infty} ^ {\ infty} f (j, k) \: g (nj, mk)$

I-filter ang pagpapatupad sa convolution

Maaari nating salain ang discrete input signal x (n) sa pamamagitan ng convolution gamit ang impulse na sagot h (n) upang makuha ang output signal y (n).

y ( n ) = x ( n ) * h ( n )

Teoryang Convolusyon

Ang Fourier na pagbabago ng isang pagpaparami ng 2 mga pag-andar ay katumbas ng pagkakabuo ng Fourier na pagbabago ng bawat pag-andar:

ℱ { f ⋅ g } = ℱ { f } * ℱ { g }

Ang Fourier transform ng isang convolution ng 2 pagpapaandar ay katumbas ng pagpaparami ng Fourier transforms ng bawat pagpapaandar:

ℱ { f * g } = ℱ { f } ⋅ ℱ { g }

Teoryang Convolution para sa tuluy-tuloy na pagbago ng Fourier

ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )

ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )

Teorema ng Convolution para sa discrete na Fourier transform

ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )

ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )

Teoryang Convolution para sa Laplace transform

ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )