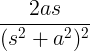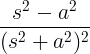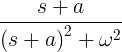Laplace Transform

Ang Laplace transform ay nagko-convert ng isang pag-andar ng oras sa domain sa pagpapa-s-domain sa pamamagitan ng pagsasama mula sa zero hanggang sa infinity

 ng pag-andar ng oras ng domain, pinarami ng e -st .

Ginamit ang Laplace transform upang mabilis na makahanap ng mga solusyon para sa mga pagkakapantay-pantay na equation at integral.

Ang paghihiwalay sa time domain ay nabago sa pagpaparami ng s sa s-domain.

Ang pagsasama sa time domain ay nabago sa paghahati ng s sa s-domain.

Pag-andar ng laplace transform

Ang Laplace transform ay tinukoy sa operator ng L {}:

F (s) = \ mathcal {L} \ kaliwa \ {f (t) \ kanan \} = \ int_ {0} ^ {\ infty} e ^ {- st} f (t) dt

Baliktarin ang Laplace transform

Ang kabaligtaran na Laplace transform ay maaaring kalkulahin nang direkta.

Karaniwan ang kabaligtaran na pagbabago ay ibinibigay mula sa talahanayan ng pagbabago.

Laplace transform table

Pangalan ng pagpapaandar Pag-andar ng oras ng domain Laplace transform

f ( t )

F ( s ) = L { f ( t )}
Patuloy 1 \ frac {1} {s}
Linear t \ frac {1} {s ^ 2}
Lakas

t n

\ frac {n!} {s ^ {n + 1}}
Lakas

t a

Γ ( a +1) ⋅ s - ( a +1)
Exponent

e sa

\ frac {1} {sa}
Sine

kasalanan sa

\ frac {a} {s ^ 2 + a ^ 2}
Cosine

cos sa

\ frac {s} {s ^ 2 + a ^ 2}
Hyperbolic sine

sinh at

\ frac {a} {s ^ 2-a ^ 2}
Hyperbolic cosine

cosh at

\ frac {s} {s ^ 2-a ^ 2}
Lumalagong sine

t kasalanan sa

\ frac {2as} {(s ^ 2 + a ^ 2) ^ 2}
Lumalaking cosine

t cos sa

\ frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2}
Nabubulok na sine

e -kahit kasalanan ωt

\ frac {\ omega} {\ kaliwa (s + a \ kanan) ^ 2 + \ omega ^ 2}
Nabubulok na cosine

e -at cos ωt

\ frac {s + a} {\ kaliwa (s + a \ kanan) ^ 2 + \ omega ^ 2}
Pag-andar ng Delta

δ ( t )

1

Naantala na delta

δ ( ta )

e -as

Ang mga katangian ng laplace ay nagbago

Pangalan ng pag-aari Pag-andar ng oras ng domain Laplace transform Magkomento
 

f ( t )

F ( s )

  
Linearity af ( t ) + bg ( t ) aF ( s ) + bG ( s ) a , b ay pare-pareho
Pagbabago ng sukat f ( sa ) \ frac {1} {a} F \ pakaliwa (\ frac {s} {a} \ kanan) isang / 0
Shift e -at f ( t ) F ( s + a )  
Pagkaantala f ( ta ) e - bilang F ( s )  
Paggaling \ frac {df (t)} {dt} sF ( s ) - f (0)  
N-derivation \ frac {d ^ nf (t)} {dt ^ n} s n f ( s ) - s n -1 f (0) - s n -2 f '(0) -...- f ( n -1) (0)  
Lakas t n f ( t ) (-1) ^ n \ frac {d ^ nF (s)} {ds ^ n}  
Pagsasama \ int_ {0} ^ {t} f (x) dx \ frac {1} {s} F (s)  
Gantihan \ frac {1} {t} f (t) \ int_ {s} ^ {\ infty} F (x) dx  
Conbolusyon f ( t ) * g ( t ) F ( s ) ⋅ G ( s ) * ay ang convolution operator
Pana-panahong pag-andar f ( t ) = f ( t + T ) \ frac {1} {1-e ^ {- sT}} \ int_ {0} ^ {T} e ^ {- sx} f (x) dx  

Mga halimbawa ng pagbabago sa laplace

Halimbawa # 1

Hanapin ang pagbabago ng f (t):

f ( t ) = 3 t + 2 t 2

Solusyon:

ℒ { t } = 1 / s 2

ℒ { t 2 } = 2 / s 3

F ( s ) = ℒ { f ( t )} = ℒ {3 t + 2 t 2 } = 3ℒ { t } + 2ℒ { t 2 } = 3 / s 2 + 4 / s 3

 

Halimbawa # 2

Hanapin ang kabaligtaran na pagbabago ng (mga) F:

F ( s ) = 3 / ( s 2 + s - 6)

Solusyon:

Upang makahanap ng kabaligtaran na pagbabago, kailangan naming baguhin ang pagpapaandar ng domain sa isang mas simpleng form:

F ( s ) = 3 / ( s 2 + s - 6) = 3 / [( s -2) ( s +3)] = a / ( s -2) + b / ( s +3)

[ a ( s +3) + b ( s -2)] / [( s -2) ( s +3)] = 3 / [( s -2) ( s +3)]

a ( s +3) + b ( s -2) = 3

Upang makahanap ng a at b, nakakakuha kami ng 2 mga equation - isa sa mga coefficients at pangalawa sa natitira:

( a + b ) s + 3 a -2 b = 3

a + b = 0, 3 a -2 b = 3

a = 3/5, b = -3/5

F ( s ) = 3/5 ( s -2) - 3/5 ( s +3)

Ngayon ang (mga) F ay madaling mababago sa pamamagitan ng paggamit ng mga talahanayan ng pagbabago para sa exponent function:

f ( t ) = (3/5) e 2 t - (3/5) e -3 t

 

Tingnan din

CALCULUS
RAPID TABLES