e pare-pareho

e pare-pareho o ang numero ng Euler ay isang pare-pareho sa matematika. Ang e pare-pareho ay totoo at hindi makatuwiran na numero.

e = 2.718281828459 ...

Kahulugan ng e
Mga pag-aari ng e
Base at logarithm
Exponential function
Formula ni Euler

Kahulugan ng e

Ang e pare-pareho ay tinukoy bilang ang limitasyon:

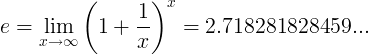
$e = \ lim_ {x \ rightarrow \ infty} \ pakaliwa (1+ \ frac {1} {x} \ kanan) ^ x = 2.718281828459 ...$

Mga kahaliling kahulugan

Ang e pare-pareho ay tinukoy bilang ang limitasyon:

$e = \ lim_ {x \ rightarrow 0} \ left (1+ \ kanan x) ^ \ frac {1} {x}$

Ang e pare-pareho ay tinukoy bilang ang walang katapusang serye:

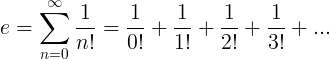
$e = \ sum_ {n = 0} ^ {\ infty} \ frac {1} {n!} = \ frac {1} {0!} + \ frac {1} {1!} + \ frac {1} { 2!} + \ Frac {1} {3!} + ...$

Mga pag-aari ng e

Gantihan ng e

Ang suklian ng e ay ang hangganan:

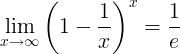
$\ lim_ {x \ rightarrow \ infty} \ pakaliwa (1- \ frac {1} {x} \ kanan) ^ x = \ frac {1} {e}$

Mga pinagmulan ng e

Ang hango ng exponential function ay ang exponential function:

( e ^x ) '= e ^x

Ang hango ng likas na pag-andar ng logarithm ay ang kapalit na paggana:

(mag-log _e x ) '= (ln x )' = 1 / x

Integral ng e

Ang indefinite integral ng exponential function e ^x ay ang exponential function e ^x .

∫ e ^x dx = e ^x + c

Ang walang katiyakan na integral ng natural na logarithm function log _e x ay:

∫ pag-log _e x dx = ∫ ln x dx = x ln x - x + c

Ang tiyak na integral mula 1 hanggang e ng katumbas na pagpapaandar na 1 / x ay 1:

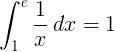
$\ int_ {1} ^ {e} \ frac {1} {x} \: dx = 1$

Base at logarithm

Ang likas na logarithm ng isang bilang x ay tinukoy bilang batayang e logarithm ng x:

ln x = log _e x

Exponential function

Ang exponential function ay tinukoy bilang:

f ( x ) = exp ( x ) = e ^x

Formula ni Euler

Ang kumplikadong numero e ^iθ ay may pagkakakilanlan:

e ^iθ = cos ( θ ) + kasalanan ko ( θ )

ako ang haka-haka na yunit (ang parisukat na ugat ng -1).

Ang θ ay anumang tunay na numero.