Likas na Logarithm - ln (x)
Ang natural na logarithm ay ang logarithm sa base e ng isang numero.
- Kahulugan ng natural na logarithm (ln)
- Mga patakaran at pag-aari ng natural na logarithm (ln)
- Masalimuot na logarithm
- Grap ng ln (x)
- Talahanayan ng natural logarithms (ln)
- Calculator ng natural logarithm
Kahulugan ng natural na logarithm
Kailan
e y = x
Pagkatapos base e logarithm ng x ay
ln ( x ) = log e ( x ) = y
Ang e pare-pareho o numero ng Euler ay:
e ≈ 2.71828183
Bilang kabaligtaran na pagpapaandar ng exponential function
Ang likas na pag-andar ng logarithm ln (x) ay ang kabaligtaran na pagpapaandar ng exponential function e x .
Para sa x/ 0,
f ( f -1 ( x )) = e ln ( x ) = x
O
f -1 ( f ( x )) = ln ( e x ) = x
Mga patakaran at pag-aari ng natural na logarithm
| Pangalan ng panuntunan | Panuntunan | Halimbawa |
|---|---|---|
Panuntunan ng produkto |
ln ( x ∙ y ) = ln ( x ) + ln ( y ) |
ln (3 ∙ 7) = ln (3) + ln (7) |
Mabilis na panuntunan |
ln ( x / y ) = ln ( x ) - ln ( y ) |
ln (3 / 7) = ln (3) - ln (7) |
Panuntunan sa kapangyarihan |
ln ( x y ) = y ∙ ln ( x ) |
ln (2 8 ) = 8 ∙ ln (2) |
ln derivative |
f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x | |
ln integral |
∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C | |
ln ng negatibong numero |
Ang ln ( x ) ay hindi natukoy kapag x ≤ 0 | |
ln ng zero |
Ang ln (0) ay hindi natukoy | |
ln ng isa |
ln (1) = 0 | |
ln ng infinity |
lim ln ( x ) = ∞, kapag x → ∞ | |
| Pagkakakilanlan ni Euler | ln (-1) = i π |
Panuntunan ng produkto ng Logarithm
Ang logarithm ng pagpaparami ng x at y ay ang kabuuan ng logarithm ng x at logarithm ng y.
mag-log b ( x ∙ y ) = mag-log b ( x ) + mag- log b ( y )
Halimbawa:
mag-log 10 (3 ∙ 7) = mag-log 10 (3) + mag- log 10 (7)
Panuntunan sa kabuuan ng Logarithm
Ang logarithm ng paghahati ng x at y ay ang pagkakaiba ng logarithm ng x at logarithm ng y.
mag-log b ( x / y ) = mag-log b ( x ) - mag- log b ( y )
Halimbawa:
mag-log 10 (3 / 7) =-log 10 (3) - log 10 (7)
Panuntunan sa kapangyarihan ng Logarithm
Ang logarithm ng x naitaas sa lakas ng y ay y na beses sa logarithm ng x.
mag-log b ( x y ) = y ∙ mag- log b ( x )
Halimbawa:
mag-log 10 (2 8 ) = 8 ∙ log 10 (2)
Hango ng natural logarithm
Ang hango ng likas na pag-andar ng logarithm ay ang pagganti na paggalaw.
Kailan
f ( x ) = ln ( x )
Ang hango ng f (x) ay:
f ' ( x ) = 1 / x
Integral ng natural logarithm
Ang integral ng natural na pag-andar ng logarithm ay ibinibigay ng:
Kailan
f ( x ) = ln ( x )
Ang integral ng f (x) ay:
∫ f ( x ) dx = ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C
Ln ng 0
Ang natural na logarithm ng zero ay hindi natukoy:
Ang ln (0) ay hindi natukoy
Ang hangganan na malapit sa 0 ng natural na logarithm ng x, kapag ang x ay papalapit sa zero, ay minus infinity:
![]()
Ln ng 1
Ang natural na logarithm ng isa ay zero:
ln (1) = 0
Ln ng infinity
Ang hangganan ng natural na logarithm ng infinity, kapag ang x ay lumalapit sa infinity ay katumbas ng infinity:
lim ln ( x ) = ∞, kapag x → ∞
Masalimuot na logarithm
Para sa kumplikadong bilang z:
z = re iθ = x + iy
Ang kumplikadong logarithm ay magiging (n = ...- 2, -1,0,1,2, ...):
Mag-log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))
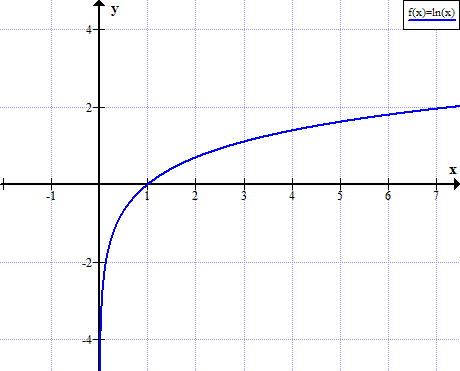
Grap ng ln (x)
Ang ln (x) ay hindi tinukoy para sa tunay na hindi positibong halaga ng x:
Talahanayan ng natural na logarithms
| x | ln x |
|---|---|
| 0 | hindi natukoy |
| 0 + | - ∞ |
| 0,0001 | -9.210340 |
| 0.001 | -6.907755 |
| 0.01 | -4.605170 |
| 0.1 | -2.302585 |
| 1 | 0 |
| 2 | 0.693147 |
| e ≈ 2.7183 | 1 |
| 3 | 1.098612 |
| 4 | 1.386294 |
| 5 | 1.609438 |
| 6 | 1.791759 |
| 7 | 1.945910 |
| 8 | 2.079442 |
| 9 | 2.197225 |
| 10 | 2.302585 |
| 20 | 2.995732 |
| 30 | 3.401197 |
| 40 | 3.688879 |
| 50 | 3.912023 |
| 60 | 4.094345 |
| 70 | 4.248495 |
| 80 | 4.382027 |
| 90 | 4.499810 |
| 100 | 4.605170 |
| 200 | 5.298317 |
| 300 | 5.703782 |
| 400 | 5.991465 |
| 500 | 6.214608 |
| 600 | 6.396930 |
| 700 | 6.551080 |
| 800 | 6.684612 |
| 900 | 6.802395 |
| 1000 | 6.907755 |
| 10000 | 9.210340 |
Tingnan din
- Logarithm (log)
- Calculator ng natural logarithm
- Likas na logarithm na zero
- Likas na logarithm ng isa
- Likas na logarithm ng e
- Likas na logarithm ng infinity
- Likas na logarithm ng negatibong numero
- Ln kabaligtaran function
- ln (x) grap
- Talahanayan ng natural na logarithm
- Calculator ng Logarithm
- e pare-pareho