İkinci dereceden denklem
İkinci dereceden denklem, 3 katsayılı ikinci dereceden bir polinomdur - a , b , c .
İkinci dereceden denklem şu şekilde verilir:
ax 2 + bx + c = 0
İkinci dereceden denklemin çözümü 2 sayı x 1 ve x 2 ile verilir .
İkinci dereceden denklemi şu şekilde değiştirebiliriz:
( x - x 1 ) ( x - x 2 ) = 0
İkinci dereceden formül
İkinci dereceden denklemin çözümü ikinci dereceden formülle verilir:
![]()
Karekök içindeki ifadeye diskriminant denir ve Δ ile gösterilir:
Δ = b 2 - 4 AC
Ayrımcı gösterime sahip ikinci dereceden formül:
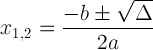
Bu ifade önemlidir çünkü bize çözüm hakkında bilgi verebilir:
- Δ/ 0 olduğunda, 2 gerçek kök vardır x 1 = (- b + √ Δ ) / (2a) ve x 2 = (- b-√ Δ ) / (2a) .
- Δ = 0 olduğunda, bir x 1 = x 2 = -b / (2a) kökü vardır .
- : Δ <0, gerçek bir kök olduğunda, 2 kompleksi kökleri bulunmaktadır
x 1 (- B + i√ = -Δ ) / (2a) ve x, 2 = (- bi√ -Δ ) / (2a) .
Sorun 1
3 x 2 +5 x +2 = 0
çözüm:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 x 3 x 2)) / (2 x 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
Sorun 2
3 x 2 -6 x + 3 = 0
çözüm:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 x 3 x 3)) / (2 x 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
Sorun 3
x 2 +2 x +5 = 0
çözüm:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 x 1 x 5)) / (2 x 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
Gerçek bir çözüm yok. Değerler karmaşık sayılardır:
x 1 = -1 + 2 ben
x 2 = -1 - 2 ben
Kuadratik Fonksiyon Grafiği
İkinci dereceden fonksiyon, ikinci dereceden bir polinom fonksiyonudur:
f ( x ) = ax 2 + bx + c
İkinci dereceden denklemin çözümleri, ikinci dereceden fonksiyon grafiğinin x ekseni ile kesişme noktaları olan ikinci dereceden fonksiyonun kökleridir.
f ( x ) = 0
Grafiğin x ekseni ile 2 kesişme noktası olduğunda, ikinci dereceden denklemin 2 çözümü vardır.
Grafiğin x ekseni ile 1 kesişme noktası olduğunda, ikinci dereceden denklemin 1 çözümü vardır.
Grafiğin x ekseni ile kesişme noktası olmadığında, gerçek çözümler (veya 2 karmaşık çözüm) elde edemeyiz.