Logaritma Kuralları
Baz b logaritma bir dizi olduğu üs Topladığımız gerektiğini tabanını numarasını almak için.
- Logaritma tanımı
- Logaritma kuralları
- Logaritma sorunları
- Karmaşık logaritma
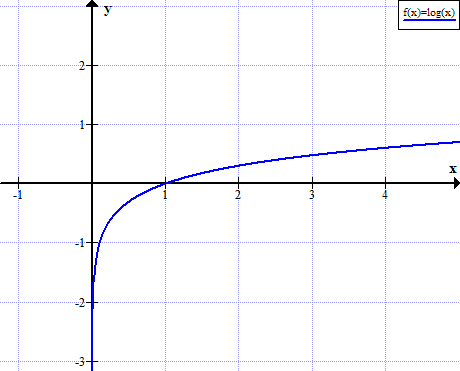
- Günlük grafiği (x)
- Logaritma tablosu
- Logaritma hesaplayıcı
Logaritma tanımı
B, y'nin kuvvetine yükseltildiğinde x'e eşittir:
b y = x
O zaman x'in taban b logaritması y'ye eşittir:
günlük b ( x ) = y
Örneğin ne zaman:
2 4 = 16
Sonra
günlük 2 (16) = 4
Üstel fonksiyonun ters fonksiyonu olarak logaritma
Logaritmik fonksiyon,
y = günlük b ( x )
üstel fonksiyonun ters fonksiyonudur,
x = b y
Dolayısıyla, x'in (x/ 0) logaritmasının üstel fonksiyonunu hesaplarsak,
f ( f -1 ( x )) = b log b ( x ) = x
Veya x'in üstel fonksiyonunun logaritmasını hesaplarsak,
f -1 ( f ( x )) = günlük b ( b x ) = x
Doğal logaritma (ln)
Doğal logaritma , e tabanına bir logaritmadır:
ln ( x ) = log e ( x )
Tüm e sabit bir sayıdır:
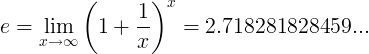
veya
![]()
Bakınız: Doğal logaritma
Ters logaritma hesaplaması
Ters logaritma (veya anti logaritma), b tabanını y logaritmasına yükselterek hesaplanır:
x = günlük -1 ( y ) = b y
Logaritmik fonksiyon
Logaritmik fonksiyonun temel biçimi şu şekildedir:
f ( x ) = günlük b ( x )
Logaritma kuralları
| Kural adı | Kural |
|---|---|
Logaritma çarpım kuralı |
log b ( x ∙ y ) = log b ( x ) + log b ( y ) |
Logaritma bölüm kuralı |
günlük b ( x / y ) = günlük b ( x ) - günlük b ( y ) |
Logaritma kuvvet kuralı |
günlük b ( x y ) = y ∙ log b ( x ) |
Logaritma temel geçiş kuralı |
log b ( c ) = 1 / log c ( b ) |
Logaritma temel değişiklik kuralı |
log b ( x ) = log c ( x ) / log c ( b ) |
Logaritmanın türevi |
f ( x ) = kütük b ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( b )) |
Logaritmanın integrali |
∫ kütük b ( x ) dx = x ∙ (kütük b ( x ) - 1 / ln ( b ) ) + C |
Negatif sayının logaritması |
x ≤ 0 olduğunda log b ( x ) tanımsızdır |
0'ın logaritması |
günlük b (0) tanımsız |
1'in logaritması |
günlük b (1) = 0 |
Tabanın logaritması |
günlük b ( b ) = 1 |
Sonsuzluğun logaritması |
lim log b ( x ) = ∞, x → ∞ olduğunda |
Bakınız: Logaritma kuralları
Logaritma çarpım kuralı
X ve y'nin çarpımının logaritması, x'in logaritması ile y'nin logaritmasının toplamıdır.
log b ( x ∙ y ) = log b ( x ) + log b ( y )
Örneğin:
günlük 10 (3 ∙ 7) = günlük 10 (3) + günlük 10 (7)
Logaritma bölüm kuralı
X ve y'nin bölünmesinin logaritması, x'in logaritması ile y'nin logaritmasının farkıdır.
günlük b ( x / y ) = günlük b ( x ) - günlük b ( y )
Örneğin:
Giriş 10 (3 / 7) = log 10 (3) - log 10 (7)
Logaritma kuvvet kuralı
X'in y'nin kuvvetine yükseltilen logaritması, y çarpı x'in logaritmasıdır.
günlük b ( x y ) = y ∙ log b ( x )
Örneğin:
günlük 10 (2 8 ) = 8 ∙ günlük 10 (2)
Logaritma temel geçiş kuralı
C'nin temel b logaritması 1 bölü b'nin c tabanlı logaritmasıdır.
log b ( c ) = 1 / log c ( b )
Örneğin:
günlük 2 (8) = 1 / günlük 8 (2)
Logaritma temel değişiklik kuralı
X'in temel b logaritması, x'in taban c logaritmasının b'nin temel c logaritmasına bölünmesiyle elde edilir.
log b ( x ) = log c ( x ) / log c ( b )
Örneğin, hesap makinesinde log 2 (8) 'i hesaplamak için, tabanı 10 olarak değiştirmemiz gerekir:
günlük 2 (8) = günlük 10 (8) / günlük 10 (2)
Bakınız: günlük bazında değişiklik kuralı
Negatif sayının logaritması
X <= 0 olduğunda x'in taban b reel logaritması, x negatif veya sıfıra eşit olduğunda tanımsızdır:
x ≤ 0 olduğunda log b ( x ) tanımsızdır
Bakınız: negatif sayının günlüğü
0'ın logaritması
Sıfırın temel b logaritması tanımsızdır:
günlük b (0) tanımsız
X sıfıra yaklaştığında, x'in taban b logaritmasının sınırı eksi sonsuzdur:
![]()
Bakınız: sıfırın günlüğü
1'in logaritması
Birin temel b logaritması sıfırdır:
günlük b (1) = 0
Örneğin, bir'in iki tabanındaki logaritması sıfırdır:
günlük 2 (1) = 0
Bakın: birinin günlüğü
Sonsuzluğun logaritması
X sonsuza yaklaştığında, x'in taban b logaritmasının sınırı sonsuza eşittir:
lim log b ( x ) = ∞, x → ∞ olduğunda
Bakınız: sonsuzluk günlüğü
Tabanın logaritması
B'nin temel b logaritması birdir:
günlük b ( b ) = 1
Örneğin, ikinin iki temel logaritması birdir:
günlük 2 (2) = 1
Logaritma türevi
Ne zaman
f ( x ) = günlük b ( x )
Sonra f (x) 'in türevi:
f ' ( x ) = 1 / ( x ln ( b ))
Bakınız: log türevi
Logaritma integrali
X'in logaritmasının integrali:
∫ kütük b ( x ) dx = x ∙ (kütük b ( x ) - 1 / ln ( b ) ) + C
Örneğin:
∫ kütük 2 ( x ) dx = x ∙ (kütük 2 ( x ) - 1 / ln (2) ) + C
Logaritma yaklaşımı
günlük 2 ( x ) ≈ n + ( x / 2 n - 1),
Karmaşık logaritma
Karmaşık sayı z için:
z = re iθ = x + iy
Karmaşık logaritma şöyle olacaktır (n = ...- 2, -1,0,1,2, ...):
Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))
Logaritma problemleri ve cevapları
Sorun 1
İçin x bulun
günlük 2 ( x ) + günlük 2 ( x -3) = 2
Çözüm:
Ürün kuralını kullanarak:
günlük 2 ( x ∙ ( x -3)) = 2
Logaritma formunu logaritma tanımına göre değiştirme:
x ∙ ( x -3) = 2 2
Veya
x 2 -3 x -4 = 0
İkinci dereceden denklemi çözme:
x 1,2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4, -1
Logaritma negatif sayılar için tanımlanmadığından yanıt şudur:
x = 4
Sorun 2
İçin x bulun
günlük 3 ( x +2) - günlük 3 ( x ) = 2
Çözüm:
Bölüm kuralını kullanarak:
günlük 3 (( x +2) / x ) = 2
Logaritma formunu logaritma tanımına göre değiştirme:
( x +2) / x = 3 2
Veya
x +2 = 9 x
Veya
8 x = 2
Veya
x = 0.25
Günlük grafiği (x)
log (x), x'in pozitif olmayan gerçek değerleri için tanımlanmamıştır:
Logaritma tablosu
| x | günlük 10 x | günlük 2 x | log e x |
|---|---|---|---|
| 0 | Tanımsız | Tanımsız | Tanımsız |
| 0 + | - ∞ | - ∞ | - ∞ |
| 0.0001 | -4 | -13.287712 | -9.210340 |
| 0.001 | -3 | -9.965784 | -6.907755 |
| 0.01 | -2 | -6.643856 | -4.605170 |
| 0.1 | -1 | -3.321928 | -2.302585 |
| 1 | 0 | 0 | 0 |
| 2 | 0.301030 | 1 | 0.693147 |
| 3 | 0.477121 | 1.584963 | 1.098612 |
| 4 | 0.602060 | 2 | 1.386294 |
| 5 | 0,698970 | 2.321928 | 1.609438 |
| 6 | 0.778151 | 2,584963 | 1.791759 |
| 7 | 0,845098 | 2.807355 | 1.945910 |
| 8 | 0.903090 | 3 | 2.079442 |
| 9 | 0.954243 | 3.169925 | 2.197225 |
| 10 | 1 | 3.321928 | 2.302585 |
| 20 | 1.301030 | 4.321928 | 2.995732 |
| 30 | 1.477121 | 4.906891 | 3.401197 |
| 40 | 1.602060 | 5,321928 | 3.688879 |
| 50 | 1.698970 | 5,643856 | 3.912023 |
| 60 | 1.778151 | 5.906991 | 4,094345 |
| 70 | 1,845098 | 6.129283 | 4.248495 |
| 80 | 1.903090 | 6,321928 | 4.382027 |
| 90 | 1.954243 | 6,491853 | 4.499810 |
| 100 | 2 | 6.643856 | 4.605170 |
| 200 | 2.301030 | 7.643856 | 5.298317 |
| 300 | 2.477121 | 8.228819 | 5.703782 |
| 400 | 2.602060 | 8.643856 | 5.991465 |
| 500 | 2.698970 | 8.965784 | 6.214608 |
| 600 | 2.778151 | 9.228819 | 6,396930 |
| 700 | 2.845098 | 9.451211 | 6.551080 |
| 800 | 2.903090 | 9.643856 | 6.684612 |
| 900 | 2.954243 | 9.813781 | 6.802395 |
| 1000 | 3 | 9.965784 | 6.907755 |
| 10000 | 4 | 13.287712 | 9.210340 |
Ayrıca bakınız
- Logaritma kuralları
- Bazın logaritma değişimi
- Sıfırın logaritması
- Birinin logaritması
- Sonsuzluğun logaritması
- Negatif sayının logaritması
- Logaritma hesaplayıcı
- Logaritma grafiği
- Logaritma tablosu
- Doğal logaritma hesaplayıcı
- Doğal logaritma - ln x
- e sabit
- Desibel (dB)