لازمی

انضمام اخذ کرنے کا الٹا عمل ہے۔

فنکشن کا انٹیگرل وہ فنکشن کے گراف کے نیچے کا علاقہ ہوتا ہے۔

غیر مطلق انٹیگرل تعریف

کب dF (x) / dx = f (x) =/ لازمی (f (x) * dx) = F (x) + c

غیر منقولہ انٹیگرل پراپرٹیز

لازمی (f (x) + g (x)) * dx = لازمی (f (x) * dx) + لازمی (g (x) * dx)

لازمی (a * f (x) * dx) = ایک * لازمی (f (x) * dx)

لازمی (f (a * x) * dx) = 1 / a * F (a * x) + c

لازمی (f (x + b) * dx) = F (x + b) + c

لازمی (f (a * x + b) * dx) = 1 / a * F (a * x + b) + c

لازمی (df (x) / dx * dx) = f (x)

انٹیگریشن متغیر کی تبدیلی

کبx = g (t) اورdx = g '(t) * dt

لازمی (f (x) * dx) = لازمی (f (g (t)) * g '(t) * dt)

حصوں کے ذریعہ انضمام

لازمی (f (x) * g '(x) * dx) = f (x) * g (x) - لازمی (f' (x) * g (x) * dx)

انٹیگرلز ٹیبل

لازمی (f (x) * dx = F (x) + c

لازمی (a * dx) = ایک * x + c

لازمی (x ^ n * dx) = 1 / (a ​​+ 1) * x ^ (a + 1) + c ، جب ایک </ - 1

لازمی (1 / x * dx) = ln (ایب (ایکس)) + سی

لازمی (e ^ x * dx) = e ^ x + c

لازمی (a ^ x * dx) = a ^ x / ln (x) + c

لازمی (ln (x) * dx) = x * ln (x) - x + c

لازمی (sin (x) * dx) = -cos (x) + c

انٹیگرل (cos (x) * dx) = sin (x) + c

لازمی (ٹین (x) * dx) = -ln (ایب (کوس (ایکس))) + سی

لازمی (آرکسن (x) * dx) = x * آرکسن (x) + مربع (1-x ^ 2) + c

لازمی (آرکاوس (x) * dx) = x * آرککوس (x) - اسکوائرٹ (1-x ^ 2) + c

لازمی (آرکٹان (x) * dx) = x * آرکٹان (x) - 1/2 * LN (1 + x ^ 2) + c

لازمی (dx / (ax + b)) = 1 / a * ln (AB (a * x + b)) + c

لازمی (1 / sqrt (a ^ 2-x ^ 2) * dx) = آرکسن (x / a) + c

لازمی (1 / sqrt (x ^ 2 + - a ^ 2) * dx) = ln (ابس (x + sqrt (x ^ 2 + - a ^ 2)) + c

لازمی (x * sqrt (x ^ 2-a ^ 2) * dx) = 1 / (a ​​* آرککوس (x / a)) + c

لازمی (1 / (a ​​^ 2 + x ^ 2) * dx) = 1 / a * آرکٹان (x / a) + c

لازمی (1 / (a ​​^ 2-x ^ 2) * dx) = 1 / 2a * ln (ابس (((a + x) / (کلہاڑی)))) + سی

لازمی (sinh (x) * dx) = کوش (x) + c

لازمی (کوش (x) * dx) = sinh (x) + c

لازمی (تنہ (x) * dx) = ln (کوش (x)) + c

 

ڈیفینیٹ انٹیگرل ڈیفینیشن

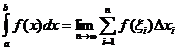
لازمی (a..b، f (x) * dx) = لم (n-/ inf، رقم (i = 1..n، f (z (i)) * dx (i)) 

کبx0 = a ، xn = b

dx (k) = x (k) - x (k-1)

x (k-1) <= z (k) <= x (k)

ڈیفینیٹ انٹیگرل حساب کتاب

کب ،

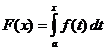 dF (x) / dx = f (x) اور

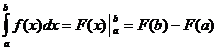
لازمی (a..b، f (x) * dx) = F (b) - F (a) 

ڈیفینیٹ انٹیگرل پراپرٹیز

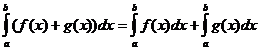
لازمی (a..b، (f (x) + g (x)) * dx) = لازمی (a..b، f (x) * dx) + لازمی (a..b، g (x) * dx )

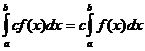
لازمی (a..b، c * f (x) * dx) = c * لازمی (a..b، f (x) * dx)

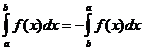
لازمی (a..b، f (x) * dx) = - لازم (b..a، f (x) * dx)

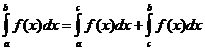
لازمی (a..b، f (x) * dx) = لازمی (a..c، f (x) * dx) + لازمی (c..b، f (x) * dx)

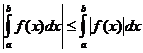
ABS (لازمی (a..b، f (x) * dx)) <= لازمی (a..b، abs (f (x)) * dx)

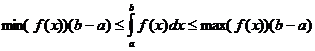منٹ (f (x)) * (با) <= لازمی (a..b، f (x) * dx) <= زیادہ سے زیادہ (f (x)) * (با) کب[ا ، بی] کے ایکس ممبر

انٹیگریشن متغیر کی تبدیلی

کبx = g (t) ،dx = g '(t) * dt ،g (alpha) = a ،جی (بیٹا) = بی

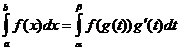
لازمی (a..b، f (x) * dx) = لازمی (الفا..بیٹا، f (g (t)) * g '(t) * dt)

حصوں کے ذریعہ انضمام

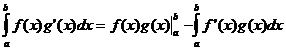
لازمی (a..b، f (x) * g '(x) * dx) = لازمی (a..b، f (x) * g (x) * dx) - لازمی (a..b، f') (x) * g (x) * dx)

مطلب قدر نظریہ

جب ایف ( ایکس ) لگاتار ہوتا ہے تو ایک نقطہ ہوتا ہےc [a، b] کا ممبر ہے تو

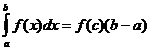
لازمی (a..b، f (x) * dx) = f (c) * (با)  

ڈیفینیٹ انٹیگرال کی ٹراپیزائڈیل قریب

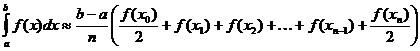
لازمی (a..b، f (x) * dx) ~ (ba) / n * (f (x (0)) / 2 + f (x (1)) + f (x (2)) + .. . + f (x (n-1)) + f (x (n)) / 2)

گاما فنکشن

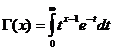
گاما (ایکس) = لازمی (0..inf، t ^ (x-1) * e ^ (- t) * dt

گاما فنکشن ایکس/ 0 کے لئے متضاد ہے ۔

گاما فنکشن پراپرٹیز

G ( x +1) = x G ( x )

G ( n +1) = n ! ، جب n ℕ (مثبت عدد)کا ممبر ہے

بیٹا فنکشن

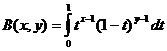
B (x، y) = لازمی (0..1، t ^ (n-1) * (1-t) ^ (y-1) * dt

بیٹا فنکشن اور گاما فنکشن ریلیشن

B (x، y) = گاما (x) * گاما (y) / گاما (x + y)

 

 

 

کیلکولس
ریپڈ ٹیبلیاں