تغیر
احتمال اور اعدادوشمار میں ، بے ترتیب متغیر کا تغیر وسط کی قیمت سے مربع فاصلے کی اوسط قیمت ہے۔ یہ اس بات کی نمائندگی کرتا ہے کہ بے ترتیب متغیر کس طرح اوسط قیمت کے قریب تقسیم کیا جاتا ہے۔ چھوٹا تغیر اس بات کی نشاندہی کرتا ہے کہ بے ترتیب متغیر اوسط قیمت کے قریب تقسیم ہوتا ہے۔ بڑا تغیر اس بات کی نشاندہی کرتا ہے کہ بے ترتیب متغیر اوسط قیمت سے بہت زیادہ تقسیم ہوتا ہے۔ مثال کے طور پر ، عام تقسیم کے ساتھ ، تنگ گھنٹی وکر میں تھوڑا سا فرق پڑے گا اور وسیع گھنٹی وکر میں بڑا فرق ہوگا۔
فرق کی تعریف
بے ترتیب متغیر X کا فرق X کے فرق کے مربع کی متوقع قیمت اور متوقع قیمت is ہے۔
σ 2 = وار ( ایکس ) = ای [( ایکس - μ ) 2 ]
تغیر کی تعریف سے جو ہم حاصل کرسکتے ہیں
σ 2 = ور ( ایکس ) = ای ( ایکس 2 ) - μ 2
مسلسل بے ترتیب متغیر کی مختلف حالتوں
اوسط قیمت with اور امکانی کثافت تقریب f (x) کے ساتھ مستقل بے ترتیب متغیر کے ل::
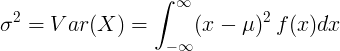
یا
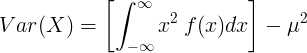
مجرد بے ترتیب متغیر کا تغیر
متوازن بے ترتیب متغیر X کے لئے جس کی قدر μ اور امکانی بڑے پیمانے پر P (x) ہو:
![]()
یا
![ور (X) = \ بائیں [\ رقم_ {i} ^ {} x_i ^ 2P (x_i) \ دائیں] - \ mu ^ 2](variance/disc_var2.gif)
متغیرات کی خصوصیات
جب X اور Y آزاد بے ترتیب متغیر ہیں:
ور ( X + Y ) = وار ( X ) + ور ( Y )
بھی دیکھو
امکان اور اعدادوشمار
ریپڈ ٹیبلیاں