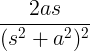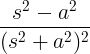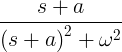Biến đổi laplace

Phép biến đổi Laplace chuyển đổi một hàm miền thời gian thành hàm miền s bằng cách tích phân từ 0 đến vô cùng

của hàm miền thời gian, nhân với e ^-st .

Phép biến đổi Laplace được sử dụng để nhanh chóng tìm ra lời giải cho các phương trình vi phân và tích phân.

Đạo hàm trong miền thời gian được chuyển thành phép nhân với s trong miền s.

Tích hợp trong miền thời gian được chuyển thành phép chia cho s trong miền s.

Hàm biến đổi Laplace

Biến đổi Laplace được xác định bằng toán tử L {}:

$F (s) = \ mathcal {L} \ left \ {f (t) \ right \} = \ int_ {0} ^ {\ infty} e ^ {- st} f (t) dt$

Biến đổi Laplace ngược có thể được tính toán trực tiếp.

Thông thường biến đổi nghịch đảo được đưa ra từ bảng biến đổi.

Tên chức năng	Hàm miền thời gian	Biến đổi laplace
Tên chức năng	f ( t )	F ( s ) = L { f ( t )}
Không thay đổi	1	$\ frac {1} {s}$
Tuyến tính	t	$\ frac {1} {s ^ 2}$
Quyền lực	t ⁿ	$\ frac {n!} {s ^ {n + 1}}$
Quyền lực	t ^a	Γ ( a +1) ⋅ s ^{- ( a +1)}
Số mũ	e ^ở	$\ frac {1} {sa}$
Sin	tội lỗi tại	$\ frac {a} {s ^ 2 + a ^ 2}$
Cô sin	cos tại	$\ frac {s} {s ^ 2 + a ^ 2}$
Sin hyperbol	sinh tại	$\ frac {a} {s ^ 2-a ^ 2}$
Cosin hyperbolic	cosh tại	$\ frac {s} {s ^ 2-a ^ 2}$
Mọc sin	t tội lỗi tại	$\ frac {2as} {(s ^ 2 + a ^ 2) ^ 2}$
Cosine đang phát triển	t cos tại	$\ frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2}$
Hình sin thối rữa	e ^-at sin ωt	$\ frac {\ omega} {\ left (s + a \ right) ^ 2 + \ omega ^ 2}$
Cosin suy giảm	e ^-at cos ωt	$\ frac {s + a} {\ left (s + a \ right) ^ 2 + \ omega ^ 2}$
Chức năng Delta	δ ( t )	1
Châu thổ bị trì hoãn	δ ( ta )	e ^-as

Tên tài sản	Hàm miền thời gian	Biến đổi laplace	Bình luận
	f ( t )	F ( s )
Tuyến tính	af ( t ) + bg ( t )	aF ( s ) + bG ( s )	a , b là hằng số
Thay đổi quy mô	f ( at )	$\ frac {1} {a} F \ left (\ frac {s} {a} \ right)$	a / 0
Shift	e ^-at f ( t )	F ( s + a )
Sự chậm trễ	f ( ta )	e ^{- as} F ( s )
Nguồn gốc	$\ frac {df (t)} {dt}$	sF ( s ) - f (0)
Dẫn xuất thứ n	$\ frac {d ^ nf (t)} {dt ^ n}$	s ⁿ f ( s ) - s ^{n -1}f (0) - s ^{n -2}f '(0) -...- f ^{( n -1)} (0)
Quyền lực	t ⁿ f ( t )	$(-1) ^ n \ frac {d ^ nF (s)} {ds ^ n}$
Hội nhập	$\ int_ {0} ^ {t} f (x) dx$	$\ frac {1} {s} F (s)$
Đối ứng	$\ frac {1} {t} f (t)$	$\ int_ {s} ^ {\ infty} F (x) dx$
Convolution	f ( t ) * g ( t )	F ( s ) ⋅ G ( s )	* là toán tử tích chập
Chức năng định kỳ	f ( t ) = f ( t + T )	$\ frac {1} {1-e ^ {- sT}} \ int_ {0} ^ {T} e ^ {- sx} f (x) dx$