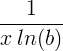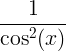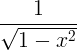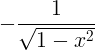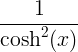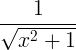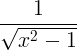导数规则
衍生规则和法律。函数的导数表。
导数定义
当Δx无限小时,函数的导数是点x +Δx和点x处函数值f(x)与Δx之差的比率。导数是函数斜率或点x处切线的斜率。
![]()
二阶导数
二阶导数由下式给出:
![]()
或者简单地导出一阶导数:
![]()
N阶导数
所述Ñ阶导数是由导出F(X)n倍来计算。
第n个导数等于(n-1)个导数的导数:
f (n)(x)= [ f (n -1)(x)]'
例:
找出的四阶导数
f(x)= 2 x 5
f (4)(x)= [2 x 5 ]''''= [10 x 4 ]'''= [40 x 3 ]''= [120 x 2 ]'= 240 x
功能图上的导数
函数的导数是切线的斜率。
导数规则
| 导数和规则 | (af(x)+ bg(x))'= af'(x)+ bg'(x) |
| 衍生产品规则 | (f(x)∙ g(x))'= f'(x)g(x)+ f(x)g'(x) |
| 导数商法则 | 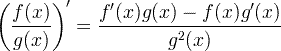 |
| 导数链规则 | f(g(x))'= f'(g(x))∙ g'(x) |
导数和规则
当a和b为常数时。
(af(x)+ bg(x))'= af'(x)+ bg'(x)
例:
查找以下项的导数:
3 x 2 + 4 x。
根据总和规则:
a = 3,b = 4
f(x)= x 2,g(x)= x
f'(x)= 2 x ,g'(x)= 1
(3 X 2 + 4 X)” =3⋅2 X +4⋅1= 6 X + 4
衍生产品规则
(f(x)∙ g(x))'= f'(x)g(x)+ f(x)g'(x)
导数商法则
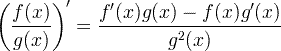
导数链规则
f(g(x))'= f'(g(x))∙ g'(x)
使用拉格朗日的符号可以更好地理解此规则:
![]()
函数线性逼近
对于小Δx,当我们知道f(x 0)和f'(x 0)时,我们可以获得f(x 0 +Δx)的近似值:
˚F(X 0 +Δ X)≈ ˚F(X 0)+ ˚F “(X 0)⋅Δ X
函数导数表
| 功能名称 | 功能 | 衍生物 |
|---|---|---|
| f(x) |
f '(x) | |
| 不变 | const |
0 |
| 线性的 | x |
1 |
| 功率 | X一 |
斧a- 1 |
| 指数的 | Ë X |
Ë X |
| 指数的 | 一个X |
一个X LN一 |
| 自然对数 | ln(x) |
|
| 对数 | 对数b(x) |
|
| 正弦波 | 罪恶x |
cos x |
| 余弦 | cos x |
-罪x |
| 切线 | 谭X |
|
| 反正弦 | 阿克辛x |
|
| 反余弦 | arccos x |
|
| 反正切 | arctan x |
|
| 双曲正弦 | 的sinh X |
cosh x |
| 双曲余弦 | cosh x |
的sinh X |
| 双曲正切 | tanh x |
|
| 反双曲正弦 | 正弦-1 x |
|
| 反双曲余弦 | cosh -1 x |
|
| 反双曲正切 | tanh -1 x |
|
衍生范例
例子1
f(x)= x 3 +5 x 2 + x +8
F' (X)= 3 X 2 +2⋅5 X + 1 + 0 = 3 X 2 10 X 1
范例#2
f(x)= sin(3 x 2)
应用链式规则时:
f'(x)= cos(3 x 2)⋅[3 x 2 ]'= cos(3 x 2)⋅6 x
二阶导数测试
当函数的一阶导数在点x 0处为零时。
f '(x 0)= 0
然后,在点x 0处的二阶导数f''(x 0)可以指示该点的类型:
| f ''(x 0)/ 0 |
局部最小值 |
| f ''(x 0)<0 |
局部最大值 |
| f ''(x 0)= 0 |
未定 |