常数
常数或欧拉数是一个数学常数。e常数是实数和无理数。
e = 2.718281828459 ...
e的定义
e常数定义为极限:
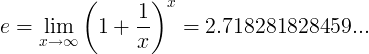
替代定义
e常数定义为极限:
![]()
e常数定义为无穷级数:
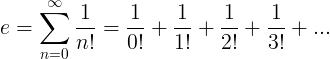
e的性质
e的倒数
e的倒数是极限:
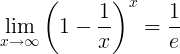
e的导数
指数函数的导数是指数函数:
(e x)'= e x
自然对数函数的导数是倒数函数:
(log e x)'=(ln x)' = 1 / x
e的积分
指数函数e x的不定积分是指数函数e x。
∫ Ë X DX = ë X + C
自然对数函数log e x的不定积分为:
∫log e x dx =∫ln x dx = x ln x-x + c
倒数函数1 / x从1到e的定积分为1:
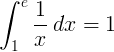
基本对数
数字x的自然对数定义为x的基本e对数:
ln x =对数e x
指数函数
指数函数定义为:
f(x)= exp(x)= e x
欧拉公式
复数Ë Iθ有身份:
Ë Iθ = COS(θ)+我SIN(θ)
i是虚数单位(-1的平方根)。
θ是任何实数。