التفاف
الالتفاف هو دالة الارتباط لـ f (τ) مع الوظيفة المعكوسة g (t-τ).
عامل الالتفاف هو رمز النجمة * .
الالتواء المستمر
إن التفاف f (t) و g (t) يساوي تكامل f (τ) مضروبًا في f (t-τ):
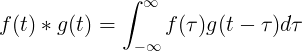
التفاف منفصل
يتم تعريف الالتفاف من وظيفتين منفصلتين على النحو التالي:
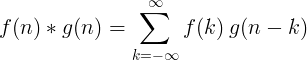
التفاف منفصل 2D
عادةً ما يتم استخدام الالتواء المنفصل ثنائي الأبعاد لمعالجة الصور.
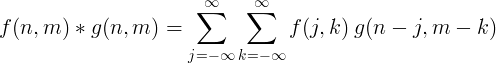
تنفيذ مرشح مع الالتواء
يمكننا تصفية إشارة الإدخال المنفصلة x (n) عن طريق الالتفاف مع الاستجابة النبضية h (n) للحصول على إشارة الخرج y (n).
ص ( ن ) = س ( ن ) * ح ( ن )
نظرية الالتواء
يساوي تحويل فورييه لمضاعفة دالتين التفاف تحويلات فورييه لكل دالة:
ℱ { f ⋅ g } = ℱ { f } * ℱ { g }
يساوي تحويل فورييه لالتفاف من وظيفتين مضاعفة تحويلات فورييه لكل دالة:
ℱ { f * g } = ℱ { f } ⋅ ℱ { g }
نظرية الالتواء لتحويل فورييه المستمر
ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )
ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )
نظرية الالتواء لتحويل فورييه المنفصل
ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )
ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )
نظرية الالتواء لتحويل لابلاس
ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )