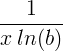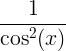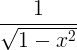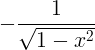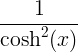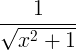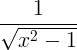القواعد المشتقة
القواعد والقوانين المشتقة. جدول مشتقات الدوال.
تعريف مشتق
مشتق الدالة هو نسبة الفرق في قيمة الدالة f (x) عند النقطتين x + Δx و x مع Δx ، عندما تكون Δx صغيرة جدًا. المشتق هو ميل الدالة أو ميل خط المماس عند النقطة x.
![]()
المشتق الثاني
يتم إعطاء المشتق الثاني بواسطة:
![]()
أو ببساطة اشتق المشتق الأول:
![]()
مشتق ن
و ن يتم احتساب عشر مشتق عن طريق اشتقاق و (خ) ن مرات.
و ن ال غير المشتقة تساوي إلى مشتق من (ن 1) مشتق:
و ( ن ) ( س ) = [ و ( ن -1) ( س )] '
مثال:
أوجد المشتق الرابع ل
و ( س ) = 2 × 5
f (4) ( x ) = [2 x 5 ] '' '= [10 x 4 ]' '' = [40 x 3 ] '' = [120 x 2 ] '= 240 x
المشتق على الرسم البياني للدالة
مشتق الدالة هو ميل الخط المماسي.
القواعد المشتقة
| قاعدة المجموع المشتق | ( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x ) |
| قاعدة المنتج المشتق | ( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x ) |
| قاعدة حاصل القسمة المشتقة | 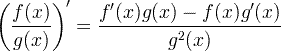 |
| قاعدة السلسلة المشتقة | f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x ) |
قاعدة المجموع المشتق
عندما يكون a و b ثوابت.
( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
مثال:
أوجد مشتق من:
3 × 2 + 4 ×.
حسب قاعدة المجموع:
أ = 3 ، ب = 4
و ( س ) = س 2 ، ز ( س ) = س
و ' ( س ) = 2 س ، ز' ( س ) = 1
(3 × 2 + 4 س ) '= 3⋅2 س + 4⋅1 = 6 س + 4
قاعدة المنتج المشتق
( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
قاعدة حاصل القسمة المشتقة
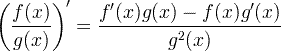
قاعدة السلسلة المشتقة
f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )
يمكن فهم هذه القاعدة بشكل أفضل باستخدام تدوين لاغرانج:
![]()
التقريب الخطي للوظيفة
بالنسبة إلى Δx الصغير ، يمكننا الحصول على تقريب لـ f (x 0 + Δx) ، عندما نعرف f (x 0 ) و f '(x 0 ):
و ( س 0 + Δ س ) ≈ و ( س 0 ) + و '( س 0 ) ⋅Δ س
جدول مشتقات الدوال
| اسم وظيفة | وظيفة | المشتق |
|---|---|---|
| و ( خ ) |
و ( س ) | |
| ثابت | مقدار ثابت |
0 |
| خطي | x |
1 |
| قوة | x أ |
الفأس أ- 1 |
| متسارع | ه س |
ه س |
| متسارع | أ س |
و س قانون الجنسية ل |
| اللوغاريتم الطبيعي | ln ( x ) |
|
| لوغاريتم | سجل ب ( خ ) |
|
| شرط | الخطيئة x |
كوس x |
| جيب التمام | كوس x |
-sin x |
| الظل | تان س |
|
| أركسين | أركسين x |
|
| أركوزين | arccos x |
|
| قوس ظل | أركتان العاشر |
|
| الجيب الزائدي | سينه س |
كوش العاشر |
| جيب التمام الزائدي | كوش العاشر |
سينه س |
| ظل زائدي | تانه س |
|
| الجيب الزائدي المعكوس | سينه -1 س |
|
| جيب التمام الزائدي المعكوس | كوش -1 × |
|
| الظل القطعي المعكوس | تانه -1 x |
|
أمثلة مشتقة
مثال 1
و ( س ) = س 3 +5 س 2 + س +8
f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1
المثال رقم 2
و ( س ) = الخطيئة (3 × 2 )
عند تطبيق قاعدة السلسلة:
f ' ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]' = cos (3 x 2 ) ⋅ 6 x
اختبار المشتق الثاني
عندما يكون المشتق الأول للدالة صفرًا عند النقطة x 0 .
و '( × 0 ) = 0
ثم المشتق الثاني عند النقطة x 0 ، f '(x 0 ) ، يمكن أن يشير إلى نوع تلك النقطة:
| f '( x 0 )/ 0 |
الحد الأدنى المحلي |
| f '( x 0 ) <0 |
الحد الأقصى المحلي |
| و '' ( × 0 ) = 0 |
غير محدد |