Квадратно уравнение
Квадратното уравнение е полином от втори ред с 3 коефициента - a , b , c .
Квадратното уравнение се дава от:
брадва 2 + bx + c = 0
Решението на квадратното уравнение се дава от 2 числа x 1 и x 2 .
Можем да променим квадратното уравнение под формата на:
( x - x 1 ) ( x - x 2 ) = 0
Квадратична формула
Решението на квадратното уравнение се дава от квадратната формула:
![]()
Изразът вътре в квадратния корен се нарича дискриминант и се обозначава с Δ:
Δ = b 2 - 4 ac
Квадратичната формула с дискриминантно означение:
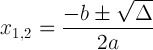
Този израз е важен, защото може да ни разкаже за решението:
- Когато Δ/ 0, има 2 реални корена x 1 = (- b + √ Δ ) / (2a) и x 2 = (- b-√ Δ ) / (2a) .
- Когато Δ = 0, има един корен x 1 = x 2 = -b / (2a) .
- Когато Δ <0, няма реални корени, има 2 сложни корена:
x 1 = (- b + i√ -Δ ) / (2a) и x 2 = (- bi√ -Δ ) / (2a) .
Проблем # 1
3 x 2 +5 x +2 = 0
решение:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
Проблем # 2
3 x 2 -6 x +3 = 0
решение:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
Проблем # 3
x 2 +2 x +5 = 0
решение:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
Няма реални решения. Стойностите са комплексни числа:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
Графика на квадратичната функция
Квадратичната функция е полиномиална функция от втори ред:
f ( x ) = ax 2 + bx + c
Решенията на квадратното уравнение са корените на квадратичната функция, които са пресечните точки на графиката на квадратичната функция с оста x, когато
f ( x ) = 0
Когато има 2 пресечни точки на графиката с оста x, има 2 решения на квадратното уравнение.
Когато има 1 пресечна точка на графиката с оста х, има 1 решение на квадратното уравнение.
Когато няма точки на пресичане на графиката с оста x, получаваме не реални решения (или 2 комплексни решения).