Правила на логаритъма
На база б логаритъм на число е степенен показател , че трябва да се повиши база , за да се получи номера.
- Определение на логаритъма
- Правила на логаритъма
- Проблеми с логаритъма
- Сложен логаритъм
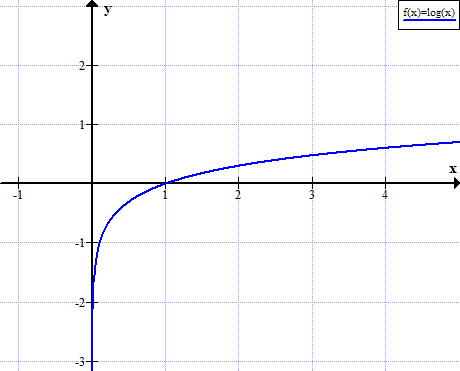
- Графика на дневника (x)
- Таблица на логаритъма
- Калкулатор на логаритъма
Определение на логаритъма
Когато b е повдигнато в степен на y е равно на x:
b y = x
Тогава основният b логаритъм на x е равен на y:
log b ( x ) = y
Например когато:
2 4 = 16
Тогава
log 2 (16) = 4
Логаритъм като обратна функция на експоненциална функция
Логаритмичната функция,
y = log b ( x )
е обратната функция на експоненциалната функция,
x = b y
Така че, ако изчислим експоненциалната функция на логаритъма на x (x/ 0),
f ( f -1 ( x )) = b log b ( x ) = x
Или ако изчислим логаритъма на експоненциалната функция на x,
f -1 ( f ( x )) = log b ( b x ) = x
Естествен логаритъм (ln)
Естественият логаритъм е логаритъм към основата e:
ln ( x ) = log e ( x )
Когато e константа е числото:
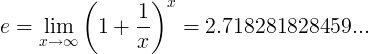
или
![]()
Вижте: Естествен логаритъм
Обратно изчисление на логаритъма
Обратният логаритъм (или анти логаритъм) се изчислява чрез издигане на основата b до логаритъма y:
x = log -1 ( y ) = b y
Логаритмична функция
Логаритмичната функция има основната форма на:
f ( x ) = log b ( x )
Правила на логаритъма
| Име на правилото | Правило |
|---|---|
Правило за логаритмен продукт |
log b ( x ∙ y ) = log b ( x ) + log b ( y ) |
Правило за коефициент на логаритъма |
log b ( x / y ) = log b ( x ) - log b ( y ) |
Правило за степента на логаритъма |
log b ( x y ) = y ∙ log b ( x ) |
Правило за превключване на логаритъма |
log b ( c ) = 1 / log c ( b ) |
Правило за промяна на логаритъма |
log b ( x ) = log c ( x ) / log c ( b ) |
Производно на логаритъма |
f ( x ) = log b ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( b )) |
Интеграл на логаритъма |
∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C |
Логаритъм на отрицателното число |
log b ( x ) е недефиниран, когато x ≤ 0 |
Логаритъм от 0 |
log b (0) е недефиниран |
Логаритъм от 1 |
log b (1) = 0 |
Логаритъм на основата |
log b ( b ) = 1 |
Логаритъм на безкрайността |
lim log b ( x ) = ∞, когато x → ∞ |
Вижте: Правила на логаритъма
Правило за логаритмен продукт
Логаритъмът на умножението на x и y е сумата от логаритъма на x и логаритъма на y.
log b ( x ∙ y ) = log b ( x ) + log b ( y )
Например:
log 10 (3 ∙ 7) = log 10 (3) + log 10 (7)
Правило за коефициент на логаритъма
Логаритъмът на разделението на x и y е разликата в логаритъма на x и логаритъма на y.
log b ( x / y ) = log b ( x ) - log b ( y )
Например:
влизане 10 (3 / 7) = влизане 10 (3) - влизане 10 (7)
Правило за степента на логаритъма
Логаритъмът на х, повдигнат до степента на у, е умножен по логаритъм от х.
log b ( x y ) = y ∙ log b ( x )
Например:
log 10 (2 8 ) = 8 ∙ log 10 (2)
Правило за превключване на логаритъма
Основният логаритъм b на c е 1, разделен на основния c логаритъм b.
log b ( c ) = 1 / log c ( b )
Например:
log 2 (8) = 1 / log 8 (2)
Правило за промяна на логаритъма
Логаритъмът на основата b на x е логаритъмът на базата на x, разделен на логаритъма на основата c на b.
log b ( x ) = log c ( x ) / log c ( b )
Например, за да изчислим дневник 2 (8) в калкулатора, трябва да променим основата на 10:
log 2 (8) = log 10 (8) / log 10 (2)
Вижте: правило за промяна на регистрационния файл
Логаритъм на отрицателното число
Реалният логаритъм b на x, когато x <= 0, е недефиниран, когато x е отрицателен или равен на нула:
log b ( x ) е недефиниран, когато x ≤ 0
Вижте: дневник на отрицателното число
Логаритъм от 0
Основният логаритъм b от нула е недефиниран:
log b (0) е недефиниран
Границата на основния b логаритъм от x, когато x се приближава до нула, е минус безкрайност:
![]()
Вижте: дневник на нулата
Логаритъм от 1
Основният логаритъм b на единица е нула:
log b (1) = 0
Например базовият два логаритъма на един е нула:
log 2 (1) = 0
Вижте: дневник на един
Логаритъм на безкрайността
Границата на основния b логаритъм от x, когато x се приближава до безкрайността, е равна на безкрайността:
lim log b ( x ) = ∞, когато x → ∞
Вижте: дневник на безкрайността
Логаритъм на основата
Основният логаритъм b на b е един:
log b ( b ) = 1
Например основният два логаритъма от две е един:
log 2 (2) = 1
Производно на логаритъма
Кога
f ( x ) = log b ( x )
Тогава производната на f (x):
f ' ( x ) = 1 / ( x ln ( b ))
Вижте: дериват на лог
Логаритъм интеграл
Интегралът на логаритъма от x:
∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C
Например:
∫ log 2 ( x ) dx = x ∙ (log 2 ( x ) - 1 / ln (2) ) + C
Приближение на логаритъма
log 2 ( x ) ≈ n + ( x / 2 n - 1),
Сложен логаритъм
За комплексно число z:
z = re iθ = x + iy
Комплексният логаритъм ще бъде (n = ...- 2, -1,0,1,2, ...):
Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · арктан ( y / x ))
Задачи и отговори на логаритъма
Проблем # 1
Намерете x за
log 2 ( x ) + log 2 ( x -3) = 2
Решение:
Използване на правилото за продукта:
log 2 ( x ∙ ( x -3)) = 2
Промяна на формата на логаритъма според дефиницията на логаритъма:
x ∙ ( x -3) = 2 2
Или
x 2 -3 x -4 = 0
Решаване на квадратното уравнение:
x 1,2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4, -1
Тъй като логаритъмът не е дефиниран за отрицателни числа, отговорът е:
x = 4
Проблем # 2
Намерете x за
log 3 ( x +2) - log 3 ( x ) = 2
Решение:
Използване на частното правило:
log 3 (( x +2) / x ) = 2
Промяна на формата на логаритъма според дефиницията на логаритъма:
( x +2) / x = 3 2
Или
x +2 = 9 x
Или
8 x = 2
Или
x = 0,25
Графика на дневника (x)
log (x) не е дефиниран за реални неположителни стойности на x:
Таблица на логаритмите
| x | log 10 x | log 2 x | log e x |
|---|---|---|---|
| 0 | неопределено | неопределено | неопределено |
| 0 + | - ∞ | - ∞ | - ∞ |
| 0,0001 | -4 | -13,287712 | -9,210340 |
| 0,001 | -3 | -9,965784 | -6.907755 |
| 0,01 | -2 | -6,643856 | -4.605170 |
| 0,1 | -1 | -3,321928 | -2.302585 |
| 1 | 0 | 0 | 0 |
| 2 | 0,301030 | 1 | 0.693147 |
| 3 | 0,477121 | 1,584963 | 1.098612 |
| 4 | 0,602060 | 2 | 1.386294 |
| 5 | 0,698970 | 2,321928 | 1.609438 |
| 6 | 0,778151 | 2.584963 | 1.791759 |
| 7 | 0,845098 | 2.807355 | 1.945910 |
| 8 | 0,903090 | 3 | 2.079442 |
| 9 | 0.954243 | 3,169925 | 2.197225 |
| 10 | 1 | 3.321928 | 2.302585 |
| 20 | 1.301030 | 4.321928 | 2.995732 |
| 30 | 1.477121 | 4.906891 | 3.401197 |
| 40 | 1.602060 | 5.321928 | 3.688879 |
| 50 | 1,698970 | 5.643856 | 3.912023 |
| 60 | 1.778151 | 5.906991 | 4.094345 |
| 70 | 1,845098 | 6.129283 | 4.248495 |
| 80 | 1.903090 | 6.321928 | 4.382027 |
| 90 | 1.954243 | 6.491853 | 4.499810 |
| 100 | 2 | 6,643856 | 4.605170 |
| 200 | 2.301030 | 7,643856 | 5.298317 |
| 300 | 2.477121 | 8,228819 | 5.703782 |
| 400 | 2,602060 | 8,643856 | 5.991465 |
| 500 | 2.698970 | 8,965784 | 6.214608 |
| 600 | 2.778151 | 9,228819 | 6.396930 |
| 700 | 2.845098 | 9.451211 | 6,551080 |
| 800 | 2.903090 | 9,643856 | 6,684612 |
| 900 | 2.954243 | 9,813781 | 6.802395 |
| 1000 | 3 | 9,965784 | 6,907755 |
| 10000 | 4 | 13.287712 | 9.210340 |
Вижте също
- Правила на логаритъма
- Промяна на логаритъма на основата
- Логаритъм от нула
- Логаритъм на едно
- Логаритъм на безкрайността
- Логаритъм на отрицателното число
- Калкулатор на логаритъма
- Графика на логаритъма
- Таблица на логаритъма
- Калкулатор с естествен логаритъм
- Естествен логаритъм - ln x
- e константа
- Децибел (dB)