Неразделна

Интеграцията е обратната операция на деривация.

Интегралът на функция е областта под графиката на функцията.

Неопределена интегрална дефиниция

Кога dF (x) / dx = f (x) =/ интеграл (f (x) * dx) = F (x) + c

Неопределени интегрални свойства

интеграл (f (x) + g (x)) * dx = интеграл (f (x) * dx) + интеграл (g (x) * dx)

интеграл (a * f (x) * dx) = a * интеграл (f (x) * dx)

интеграл (f (a * x) * dx) = 1 / a * F (a * x) + c

интеграл (f (x + b) * dx) = F (x + b) + c

интеграл (f (a * x + b) * dx) = 1 / a * F (a * x + b) + c

интеграл (df (x) / dx * dx) = f (x)

Промяна на променливата на интеграцията

Когаx = g (t) иdx = g '(t) * dt

интеграл (f (x) * dx) = интеграл (f (g (t)) * g '(t) * dt)

Интегриране по части

интеграл (f (x) * g '(x) * dx) = f (x) * g (x) - интеграл (f' (x) * g (x) * dx)

Таблица на интегралите

интеграл (f (x) * dx = F (x) + c

интеграл (a * dx) = a * x + c

интеграл (x ^ n * dx) = 1 / (a ​​+ 1) * x ^ (a + 1) + c, когато a </ - 1

интеграл (1 / x * dx) = ln (abs (x)) + c

интеграл (e ^ x * dx) = e ^ x + c

интеграл (a ^ x * dx) = a ^ x / ln (x) + c

интеграл (ln (x) * dx) = x * ln (x) - x + c

интеграл (sin (x) * dx) = -cos (x) + c

интеграл (cos (x) * dx) = sin (x) + c

интеграл (tan (x) * dx) = -ln (abs (cos (x))) + c

интеграл (arcsin (x) * dx) = x * arcsin (x) + sqrt (1-x ^ 2) + c

интеграл (arccos (x) * dx) = x * arccos (x) - sqrt (1-x ^ 2) + c

интеграл (arctan (x) * dx) = x * arctan (x) - 1/2 * ln (1 + x ^ 2) + c

интеграл (dx / (ax + b)) = 1 / a * ln (abs (a * x + b)) + c

интеграл (1 / sqrt (a ^ 2-x ^ 2) * dx) = arcsin (x / a) + c

интеграл (1 / sqrt (x ^ 2 + - a ^ 2) * dx) = ln (abs (x + sqrt (x ^ 2 + - a ^ 2)) + c

интеграл (x * sqrt (x ^ 2-a ^ 2) * dx) = 1 / (a ​​* arccos (x / a)) + c

интеграл (1 / (a ​​^ 2 + x ^ 2) * dx) = 1 / a * arctan (x / a) + c

интеграл (1 / (a ​​^ 2-x ^ 2) * dx) = 1 / 2a * ln (abs (((a + x) / (ax))) + c

интеграл (sinh (x) * dx) = cosh (x) + c

интеграл (cosh (x) * dx) = sinh (x) + c

интеграл (tanh (x) * dx) = ln (cosh (x)) + c

 

Определена интегрална дефиниция

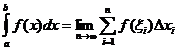
интеграл (a..b, f (x) * dx) = lim (n-/ inf, сума (i = 1..n, f (z (i)) * dx (i))) 

Когаx0 = a, xn = b

dx (k) = x (k) - x (k-1)

x (k-1) <= z (k) <= x (k)

Определено интегрално изчисление

Кога ,

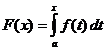 dF (x) / dx = f (x) и

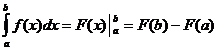
интеграл (a..b, f (x) * dx) = F (b) - F (a) 

Определени интегрални свойства

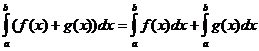
интеграл (a..b, (f (x) + g (x)) * dx) = интеграл (a..b, f (x) * dx) + интеграл (a..b, g (x) * dx )

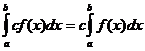
интеграл (a..b, c * f (x) * dx) = c * интеграл (a..b, f (x) * dx)

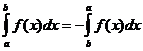
интеграл (a..b, f (x) * dx) = - интеграл (b..a, f (x) * dx)

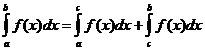
интеграл (a..b, f (x) * dx) = интеграл (a..c, f (x) * dx) + интеграл (c..b, f (x) * dx)

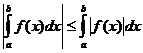
abs (интеграл (a..b, f (x) * dx)) <= интеграл (a..b, abs (f (x)) * dx)

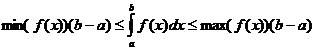min (f (x)) * (ba) <= интеграл (a..b, f (x) * dx) <= max (f (x)) * (ba) когаx член на [a, b]

Промяна на променливата на интеграцията

Когаx = g (t) ,dx = g '(t) * dt ,g (алфа) = a ,g (бета) = b

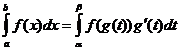
интеграл (a..b, f (x) * dx) = интеграл (алфа..бета, f (g (t)) * g '(t) * dt)

Интегриране по части

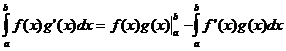
интеграл (a..b, f (x) * g '(x) * dx) = интеграл (a..b, f (x) * g (x) * dx) - интеграл (a..b, f' (x) * g (x) * dx)

Теорема за средната стойност

Когато f ( x ) е непрекъснато, има точкаc е член на [a, b] така

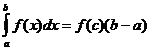
интеграл (a..b, f (x) * dx) = f (c) * (ba)  

Трапецовидна апроксимация на определен интеграл

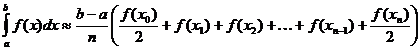
интеграл (a..b, f (x) * dx) ~ (ba) / n * (f (x (0)) / 2 + f (x (1)) + f (x (2)) + .. . + f (x (n-1)) + f (x (n)) / 2)

Гама функцията

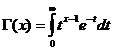
гама (x) = интеграл (0..inf, t ^ (x-1) * e ^ (- t) * dt

Гама функцията е конвергентна при x/ 0 .

Свойства на гама функция

G ( x +1) = x G ( x )

G ( n +1) = n ! , когато n ℕ (положително цяло число).е член на

Бета функцията

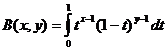
B (x, y) = интеграл (0..1, t ^ (n-1) * (1-t) ^ (y-1) * dt

Бета функция и връзка с гама функция

B (x, y) = гама (x) * гама (y) / гама (x + y)

 

 

 

КАЛКУЛ
БЪРЗИ МАСИ