দ্বিঘাত সমীকরণ
চতুর্ভুজ সমীকরণটি একটি দ্বিতীয় ক্রমের বহুবর্ষ যা 3 সহগ সহ - ক , খ , গ ।
চতুর্ভুজ সমীকরণটি প্রদান করেছেন:
অক্ষ 2 + বিএক্স + সি = 0
চতুর্ভুজ সমীকরণের সমাধানটি 2 সংখ্যা x 1 এবং x 2 দিয়ে দেওয়া হয়েছে ।
আমরা চতুর্ভুজ সমীকরণটি আকারে পরিবর্তন করতে পারি:
( x - x 1 ) ( x - x 2 ) = 0
দ্বিঘাত সূত্র
চতুর্ভুজ সমীকরণের সমাধানটি চতুষ্কোণ সূত্রে দেওয়া হয়েছে:
![]()
বর্গমূলের অভ্যন্তরের প্রকাশকে বৈষম্যমূলক বলা হয় এবং Δ দ্বারা চিহ্নিত করা হয়:
Δ = খ 2 - 4 এসি
বৈষম্যমূলক স্বরলিপি সহ চতুর্ভুজ সূত্র:
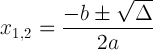
এই অভিব্যক্তিটি গুরুত্বপূর্ণ কারণ এটি সমাধান সম্পর্কে আমাদের জানাতে পারে:
- যখন Δ/ 0, সেখানে দুটি আসল শিকড় থাকে x 1 = (- বি + √ Δ ) / (2 এ) এবং এক্স 2 = (- বি-√ Δ ) / (2 এ) ।
- যখন Δ = 0 হয়, সেখানে একটি রুট x 1 = x 2 = -b / (2a) থাকে ।
- যখন Δ <0, কোনও আসল শিকড় থাকে না, সেখানে দুটি জটিল শিকড় থাকে:
x 1 = (- b + i√ -Δ ) / (2a) এবং x 2 = (- বিআই -Δ ) / (2 এ) ।
সমস্যা # 1
3 এক্স 2 +5 x +2 = 0
সমাধান:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
সমস্যা # 2
3 এক্স 2 -6 এক্স +3 = 0
সমাধান:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
সমস্যা # 3
x 2 + 2 x +5 = 0
সমাধান:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
কোন বাস্তব সমাধান আছে। মানগুলি জটিল সংখ্যা:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
চতুর্ভুজ ফাংশন গ্রাফ
চতুর্ভুজ ফাংশন একটি দ্বিতীয় ক্রম বহুপদী ফাংশন:
f ( x ) = ax 2 + bx + c
চতুর্ভুজ সমীকরণের সমাধানগুলি হ'ল চতুর্ভুজ ফাংশনের মূলগুলি, যা এক্স-অক্ষের সাথে চতুর্ভুজ ফাংশন গ্রাফের ছেদ বিন্দু হয়, যখন
f ( x ) = 0
এক্স-অক্ষের সাথে যখন গ্রাফের 2 ছেদ পয়েন্ট থাকে, তখন চতুর্ভুজ সমীকরণের 2 টি সমাধান রয়েছে।
এক্স-অক্ষের সাথে যখন গ্রাফের 1 ছেদ বিন্দু থাকে তখন চতুর্ভুজ সমীকরণের 1 সমাধান থাকে।
যখন এক্স-অক্ষের সাথে গ্রাফের কোনও ছেদ বিন্দু না থাকে, আমরা প্রকৃত সমাধান (বা 2 জটিল সমাধান) পাই না।