লোগারিদম বিধি

বেস খ লগারিদম একটি সংখ্যা হয় এক্সপোনেন্ট যে আমরা বাড়াতে প্রয়োজন বেস অর্ডার নম্বর পেতে হবে।

লোগারিদম সংজ্ঞা

খ যখন y এর শক্তিতে উত্থাপিত হয় সমান x:

খ y = x

তারপরে x এর বেস খ লোগারিদম y এর সমান:

লগ বি ( এক্স ) = y

উদাহরণস্বরূপ যখন:

2 4 = 16

তারপরে

লগ 2 (16) = 4

তাত্পর্যপূর্ণ ফাংশনের বিপরীত ফাংশন হিসাবে লগারিদম

লগারিদমিক ফাংশন,

y = লগ খ ( এক্স )

সূচকীয় ফাংশনের বিপরীত ফাংশন,

x = খ y

সুতরাং আমরা যদি x (x/ 0) এর লগারিদমটির সূচকীয় ফাংশন গণনা করি,

f ( f -1 ( x )) = b লগ বি ( x ) = x

বা যদি আমরা এক্স এর এক্সফোনেনশিয়াল ফাংশনের লগারিদম গণনা করি,

f -1 ( f ( x )) = লগ বি ( বি এক্স ) = এক্স

প্রাকৃতিক লোগারিদম (এলএন)

প্রাকৃতিক লোগারিদম হল বেস ই এর লোগারিদম

ln ( x ) = লগ ই ( এক্স )

যখন ই ধ্রুবকটি সংখ্যা হয়:

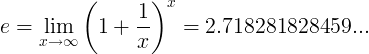
e = \ lim_ {x \ rightarrow \ infty} \ বাম (1+ \ frac {1} {x} \ ডান) ^ x = 2.718281828459 ...

বা

e = \ lim_ {x \ রাইটারো 0} \ বাম (1+ \ ডান এক্স) ^ rac frac {1} {x}

 

দেখুন: প্রাকৃতিক লগারিদম

বিপরীত লগারিদম গণনা

বিপরীত লোগারিদম (বা বিরোধী লোগারিদম) বেস বেসকে লগারিদম y তে বাড়িয়ে গণনা করা হয়:

x = লগ -1 ( y ) = বি y

লোগারিদমিক ফাংশন

লগারিদমিক ফাংশনটির মূল ফর্ম রয়েছে:

f ( x ) = লগ বি ( এক্স )

লোগারিদম বিধি

বিধি নাম নিয়ম
লোগারিদম পণ্য বিধি
 লগ বি ( x ∙ y ) = লগ বি ( এক্স ) + লগ বি ( y )
লোগারিদম ভাগফলের নিয়ম
 লগ বি ( x / y ) = লগ বি ( এক্স ) - লগ বি ( y )
লোগারিদম শক্তি বিধি
 লগ বি ( x y ) = y ∙ লগ বি ( এক্স )
লোগারিদম বেস স্যুইচ নিয়ম
 লগ বি ( সি ) = 1 / লগ সি ( খ )
লোগারিদম বেস পরিবর্তন নিয়ম
 লগ বি ( এক্স ) = লগ সি ( এক্স ) / লগ সি ( খ )
লগারিদম এর ডেরাইভেটিভ
 f ( x ) = লগ বি ( এক্স ) ⇒ ফ ' ( এক্স ) = 1 / ( এক্স এলএন ( খ ))
লোগারিদমের ইন্টিগ্রাল
 ∫ লগ বি ( এক্স ) ডিএক্স = এক্স ∙ (লগ বি ( এক্স ) - 1 / এলএন ( বি ) ) + সি
Negativeণাত্মক সংখ্যার লোগারিদম
 লগ খ ( এক্স ) undefined যখন এক্স ≤ 0
লোগারিদম 0
 লগ বি (0) নির্ধারিত
\ lim_ {x \ থেকে 0 ^ +} \ টেক্সটআপ {লগ} _ বি (এক্স) = - \ ইনফটি
লোগারিদম 1
 লগ বি (1) = 0
বেসের লোগারিদম
 লগ খ ( খ ) = 1
অনন্তের লোগারিদম
 লিম লগ বি ( x ) = ∞, যখন x → ∞ ∞

দেখুন: লোগারিদম বিধি

 

লোগারিদম পণ্য বিধি

X এবং y এর গুণনের লগারিদম হল x এর লোগারিদমের যোগফল এবং y এর লোগারিদমের সমষ্টি।

লগ বি ( x ∙ y ) = লগ বি ( এক্স ) + লগ বি ( y )

উদাহরণ স্বরূপ:

লগ 10 (3 ∙ 7) = লগ 10 (3) + লগ 10 (7)

লোগারিদম ভাগফলের নিয়ম

X এবং y এর বিভাজনের লগারিদম হ'ল x এর লোগারিদম এবং y এর লোগারিদমের পার্থক্য।

লগ বি ( x / y ) = লগ বি ( এক্স ) - লগ বি ( y )

উদাহরণ স্বরূপ:

লগ ইন করুন 10 (3 / 7) = log 10 (3) - লগ ইন করুন 10 (7)

লোগারিদম শক্তি বিধি

X এর লোগারিদম y এর ক্ষমতায় উত্থাপিত x এর লোগারিদমের y গুন।

লগ বি ( x y ) = y ∙ লগ বি ( এক্স )

উদাহরণ স্বরূপ:

লগ 10 (2 8 ) = 8 ∙ লগ 10 (2)

লোগারিদম বেস স্যুইচ নিয়ম

গ এর বেস বি লোগারিদম 1 টি খ এর বেস সি লোগারিদম দ্বারা বিভক্ত হয়।

লগ বি ( সি ) = 1 / লগ সি ( খ )

উদাহরণ স্বরূপ:

লগ 2 (8) = 1 / লগ 8 (2)

লোগারিদম বেস পরিবর্তন নিয়ম

X এর বেস বি লোগারিদম হল x এর বেস সি লোগারিদম খ এর বেস সি লোগারিদম দ্বারা বিভক্ত।

লগ বি ( এক্স ) = লগ সি ( এক্স ) / লগ সি ( খ )

উদাহরণস্বরূপ, ক্যালকুলেটরে লগ 2 (8) গণনা করার জন্য , আমাদের বেসটি 10 ​​এ পরিবর্তন করা দরকার:

লগ 2 (8) = লগ 10 (8) / লগ 10 (2)

দেখুন: লগ বেস পরিবর্তন নিয়ম

Negativeণাত্মক সংখ্যার লোগারিদম

X এর বেস বি আসল লগারিদম যখন x <= 0 অপরিজ্ঞাত হয় যখন x negativeণাত্মক বা শূন্যের সমান হয়:

লগ খ ( এক্স ) undefined যখন এক্স ≤ 0

দেখুন: negativeণাত্মক সংখ্যা লগ

লোগারিদম 0

শূন্যের বেস বি লোগারিদম অপরিজ্ঞাত:

লগ বি (0) নির্ধারিত

X এর বেস বি লোগারিদমের সীমা, যখন x শূন্যের নিকটে আসে, বিয়োগ অনন্ত:

\ lim_ {x \ থেকে 0 ^ +} \ টেক্সটআপ {লগ} _ বি (এক্স) = - \ ইনফটি

দেখুন: শূন্য লগ

লোগারিদম 1

একটির বেস বি লোগারিদম শূন্য:

লগ বি (1) = 0

উদাহরণস্বরূপ, তেহ বেস দুটি লগারিদম একের শূন্য:

লগ 2 (1) = 0

দেখুন: একটি লগ

অনন্তের লোগারিদম

X এর বেস বি লোগারিদমের সীমা, যখন x অনন্তের কাছে পৌঁছায়, অনন্তের সমান:

লিম লগ বি ( x ) = ∞, যখন x → ∞ ∞

দেখুন: অনন্ত লগ

বেসের লোগারিদম

খ এর বেস বি লোগারিদম এক:

লগ খ ( খ ) = 1

উদাহরণস্বরূপ, দুইটির বেস দুটি লোগারিদম হ'ল:

লগ 2 (2) = 1

লোগারিদম ডেরিভেটিভ

কখন

f ( x ) = লগ বি ( এক্স )

তারপরে চ (এক্স) এর ডেরাইভেটিভ:

f ' ( x ) = 1 / ( এক্স এলএন ( খ ))

দেখুন: লগ ডেরাইভেটিভ

লোগারিদম অবিচ্ছেদ্য

এক্স এর লোগারিদমের অবিচ্ছেদ্য:

∫ লগ বি ( এক্স ) ডিএক্স = এক্স ∙ (লগ বি ( এক্স ) - 1 / এলএন ( বি ) ) + সি

উদাহরণ স্বরূপ:

∫ লগ 2 ( এক্স ) ডিএক্স = এক্স ∙ (লগ 2 ( এক্স ) - 1 / এলএন (2) ) + সি

লোগারিদম আনুমানিক

লগ 2 ( x ) ≈ n + ( এক্স / 2 এন - 1),

জটিল লগারিদম

জটিল সংখ্যা z এর জন্য:

z = re iθ = x + iy

জটিল লোগারিদম হবে (n = ...- 2, -1,0,1,2, ...):

লগ z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · আর্টিকান ( y / x ))

লোগারিদম সমস্যা এবং উত্তর

সমস্যা # 1

জন্য এক্স সন্ধান করুন

লগ 2 ( এক্স ) + লগ 2 ( এক্স -3) = 2

সমাধান:

পণ্য বিধি ব্যবহার:

লগ 2 ( x ∙ ( এক্স -3)) = 2

লগারিদম সংজ্ঞা অনুসারে লোগারিদম ফর্ম পরিবর্তন করা:

x ∙ ( x -3) = 2 2

বা

x 2 -3 x -4 = 0

চতুর্ভুজ সমীকরণ সমাধান:

x 1,2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4, -1

যেহেতু লগারিদমটি নেতিবাচক সংখ্যার জন্য সংজ্ঞায়িত করা হয়নি, উত্তরটি হ'ল:

x = 4

সমস্যা # 2

জন্য এক্স সন্ধান করুন

লগ 3 ( x +2) - লগ 3 ( এক্স ) = 2

সমাধান:

ভাগফলের নিয়ম ব্যবহার করে:

লগ 3 (( x +2) / এক্স ) = 2

লগারিদম সংজ্ঞা অনুসারে লোগারিদম ফর্ম পরিবর্তন করা:

( x +2) / এক্স = 3 2

বা

x +2 = 9 x

বা

8 এক্স = 2

বা

x = 0.25

লগের গ্রাফ (এক্স)

লগ (এক্স) এক্স এর বাস্তব অ-ধনাত্মক মানের জন্য সংজ্ঞায়িত করা হয়নি:

লোগারিদম টেবিল

এক্স লগ 10 এক্স লগ 2 এক্স লগ ই x
0 অপরিবর্তিত অপরিবর্তিত অপরিবর্তিত
0 + - ∞ - ∞ - ∞
0.0001 -4 -13.287712 -9.210340
0.001 -৩ -9.965784 -6.907755
0.01 -২ -6.643856 -4.605170
0.1 -1 -3.321928 -2.302585
1 0 0 0
2 0.301030 1 0.693147
3 0.477121 1.584963 1.098612
4 0.602060 2 1.386294
5 0.698970 2.321928 1.609438
6 0.778151 2.584963 1.791759
7 0.845098 2.807355 1.945910
8 0.903090 3 2.079442
9 0.954243 3.169925 2.197225
10 1 3.321928 2.302585
20 1.301030 4.321928 2.995732
30 1.477121 4.906891 3.401197
40 1.602060 5.321928 3.688879
50 1.698970 5.643856 3.912023
60 1.778151 5.906991 4.094345
70 1.845098 6.129283 4.248495
80 1.903090 6.321928 4.382027
90 1.954243 6.491853 4.499810
100 2 6.643856 4.605170
200 2.301030 7.643856 5.298317
300 2.477121 8.228819 5.703782
400 2.602060 8.643856 5.991465
500 2.698970 8.965784 6.214608
600 2.778151 9.228819 6.396930
700 2.845098 9.451211 6.551080
800 2.903090 9.643856 6.684612
900 2.954243 9.813781 6.802395
1000 3 9.965784 6.907755
10000 4 13.287712 9.210340

 

লোগারিদম ক্যালকুলেটর ►

 

আরো দেখুন

ALGEBRA
দ্রুত টেবিল