ইন্টিগ্রাল

একীকরণ হ'ল ডাইরিভিশনের বিপরীত অপারেশন।

কোনও ফাংশনের ইন্টিগ্রাল হ'ল ফাংশনের গ্রাফের নীচে অঞ্চল area

অনির্দিষ্ট ইন্টিগ্রাল সংজ্ঞা

কখন dF (x) / dx = f (x) =/ অবিচ্ছেদ্য (f (x) * dx) = F (x) + c

অনির্দিষ্ট ইন্টিগ্রাল প্রোপার্টি

ইন্টিগ্রাল (f (x) + g (x)) * dx = ইন্টিগ্রাল (f (x) * dx) + ইন্টিগ্রাল (g (x) * dx)

অবিচ্ছেদ্য (a * f (x) * dx) = a * অবিচ্ছেদ্য (f (x) * dx)

ইন্টিগ্রাল (এফ (এ * এক্স) * ডিএক্স) = 1 / এ * এফ (এ * এক্স) + সি

ইন্টিগ্রাল (এফ (এক্স + বি) * ডিএক্স) = এফ (এক্স + বি) + সি

অবিচ্ছেদ্য (এফ (এ * এক্স + বি) * ডিএক্স) = 1 / এ * এফ (এ * এক্স + বি) + সি

অবিচ্ছেদ্য (df (x) / dx * dx) = f (x)

একীকরণের পরিবর্তনশীল পরিবর্তনযোগ্য

কখনx = g (টি) এবংdx = g '(t) * dt

ইন্টিগ্রাল (f (x) * dx) = ইন্টিগ্রাল (f (g (t)) * g '(t) * dt)

অংশ দ্বারা সংহত

অবিচ্ছেদ্য (f (x) * g '(x) * dx) = f (x) * g (x) - অবিচ্ছেদ্য (f' (x) * g (x) * dx)

ইন্টিগ্রালস টেবিল

অবিচ্ছেদ্য (f (x) * dx = F (x) + গ

ইন্টিগ্রাল (a * dx) = a * x + c

অবিচ্ছেদ্য (x ^ n * dx) = 1 / (a ​​+ 1) * x ^ (a + 1) + সি, যখন <</ - 1

অবিচ্ছেদ্য (1 / x * dx) = ln (অ্যাবস (এক্স)) + সি

অবিচ্ছেদ্য (e ^ x * dx) = ই ^ x + সি

ইন্টিগ্রাল (a ^ x * dx) = a ^ x / ln (x) + c

ইন্টিগ্রাল (ln (x) * dx) = x * ln (x) - x + c

ইন্টিগ্রাল (sin (x) * dx) = -cos (x) + c

ইন্টিগ্রাল (cos (x) * dx) = sin (x) + c

ইন্টিগ্রাল (ট্যান (x) * dx) = -ln (অ্যাবস (কোস (এক্স))) + সি

ইন্টিগ্রাল (আরকসিন (এক্স) * ডিএক্স) = এক্স * আরকসিন (এক্স) + স্কয়ার্ট (1-এক্স ^ 2) + সি

অবিচ্ছেদ্য (আরকোস (এক্স) * ডিএক্স) = এক্স * আরকোস (এক্স) - স্কয়ার্ট (1-x ^ 2) + সি

অবিচ্ছেদ্য (আর্টিকান (এক্স) * ডেক্স) = এক্স * আর্টিকান (এক্স) - 1/2 * এলএন (1 + x ^ 2) + সি

অবিচ্ছেদ্য (dx / (ax + b)) = 1 / a * ln (অ্যাবস (এ * এক্স + বি)) + সি

অবিচ্ছেদ্য (1 / বর্গক্ষেত্র (a ^ 2-x ^ 2) * dx) = আরকসিন (এক্স / এ) + সি

অবিচ্ছেদ্য (1 / বর্গক্ষেত্র (x + 2 + - a ^ 2) * dx) = ln (অ্যাবস (x + sqrt (x ^ 2 + - একটি ^ 2)) + সি

অবিচ্ছেদ্য (x * স্কয়ার্ট (x ^ 2-a ^ 2) * dx) = 1 / (একটি * আরকোস (এক্স / এ)) + সি

অবিচ্ছেদ্য (1 / (a ​​^ 2 + x ^ 2) * dx) = 1 / a * আর্টিকান (x / a) + সি

অবিচ্ছেদ্য (1 / (a ​​^ 2-x ^ 2) * dx) = 1 / 2a * ln (অ্যাবস (((একটি + এক্স) / (কুড়াল)))) + সি

ইন্টিগ্রাল (sinh (x) * dx) = cosh (x) + c

ইন্টিগ্রাল (cosh (x) * dx) = sinh (x) + c

ইন্টিগ্রাল (তানহ (এক্স) * ডেক্স) = এলএন (কোশ (এক্স)) + সি

 

ডিফিনিট ইন্টিগ্রাল সংজ্ঞা

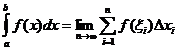
অবিচ্ছেদ্য (a..b, f (x) * dx) = lim (n-/ inf, যোগফল (i = 1..n, f (z (i)) * dx (i)) 

কখনx0 = এ, এক্সএন = খ

dx (কে) = x (কে) - এক্স (কে -1)

x (কে -1) <= জেড (কে) <= এক্স (কে)

ডিফিনিট ইন্টিগ্রাল গণনা

কখন ,

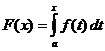 dF (x) / dx = f (x) এবং

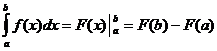
অবিচ্ছেদ্য (a..b, f (x) * dx) = F (b) - F (a) 

নির্ধারিত ইন্টিগ্রাল প্রোপার্টি

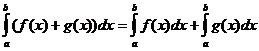
অবিচ্ছেদ্য (a..b, (f (x) + g (x)) * dx) = ইন্টিগ্রাল (a..b, f (x) * dx) + ইন্টিগ্রাল (a..b, g (x) * dx )

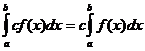
অবিচ্ছেদ্য (a..b, c * f (x) * dx) = c * অবিচ্ছেদ্য (a..b, f (x) * dx)

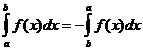
ইন্টিগ্রাল (a..b, f (x) * dx) = - ইন্টিগ্রাল (b..a, f (x) * dx)

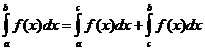
ইন্টিগ্রাল (a..b, f (x) * dx) = ইন্টিগ্রাল (a..c, f (x) * dx) + ইন্টিগ্রাল (c..b, f (x) * dx)

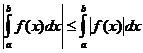
ABS (অবিচ্ছেদ্য (a..b, f (x) * dx)) <= অবিচ্ছেদ্য (a..b, অ্যাবস (চ (এক্স)) * dx)

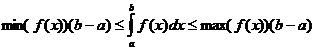মিনিট (চ (এক্স)) * (বা) <= অবিচ্ছেদ্য (a..b, f (x) * dx) <= সর্বোচ্চ (চ (এক্স)) * (বা) কখন[এ, বি] এর এক্স সদস্য

একীকরণের পরিবর্তনশীল পরিবর্তনযোগ্য

কখনx = g (টি) ,dx = g '(t) * dt ,g (আলফা) = ক ,g (বিটা) = খ

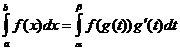
অবিচ্ছেদ্য (a..b, f (x) * dx) = ইন্টিগ্রাল (আলফা..বেতা, চ (জি (টি)) * জি '(টি) * ডিটি)

অংশ দ্বারা সংহত

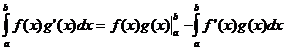
ইন্টিগ্রাল (a..b, f (x) * g '(x) * dx) = ইন্টিগ্রাল (a..b, f (x) * g (x) * dx) - ইন্টিগ্রাল (a..b, f') (x) * g (x) * dx)

গড় মান উপপাদ্য

যখন f ( x ) অবিচ্ছিন্ন থাকে তখন একটি বিন্দু থাকেসি [এ, বি] এর সদস্য তাই

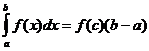
অবিচ্ছেদ্য (a..b, f (x) * dx) = f (c) * (বা)  

ট্রাইফিজয়েডাল আনুমানিক সংজ্ঞা

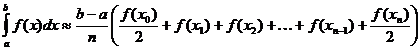
অবিচ্ছেদ্য (a..b, f (x) * dx) ~ (ba) / n * (f (x (0)) / 2 + f (x (1)) + f (x (2)) + .. । + f (x (n-1)) + f (x (n)) / 2)

গামা ফাংশন

গামা (এক্স) = অবিচ্ছেদ্য (0..ইনফ, টি ^ (এক্স -1) * ই ^ (- টি) * ডিটি

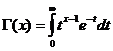
গামা ফাংশনটি এক্স/ 0 এর জন্য অভিজাত ।

গামা ফাংশন বৈশিষ্ট্য

জি ( x +1) = x জি ( এক্স )

জি ( এন +1) = এন ! , যখন এন ℕ (ধনাত্মক পূর্ণসংখ্যা)।এর সদস্য

বিটা ফাংশন

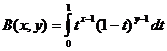
বি (এক্স, ওয়াই) = অবিচ্ছেদ্য (০.১.২, টি ^ (এন -১) * (১-টি) ^ (ওয়াই -১) * ডিটি

বিটা ফাংশন এবং গামা ফাংশন রিলেশন

বি (এক্স, ই) = গামা (এক্স) * গামা (y) / গামা (এক্স + ই)

 

 

 

ক্যালকুলাস
দ্রুত টেবিল