ফিবোনাচি নাম্বার এবং সিকোয়েন্স
ফিবোনাচি সিকোয়েন্স হ'ল সংখ্যার ক্রম, যেখানে প্রতিটি সংখ্যা 0 এবং 1 হ'ল প্রথম দুটি সংখ্যা ব্যতীত 2 পূর্ববর্তী সংখ্যার যোগফল।
- ফিবোনাচি সিকোয়েন্স সূত্র
- গোল্ডেন রেশিও কনভার্জেন্স
- ফিবোনাচি সিকোয়েন্স টেবিল
- ফিবোনাচি সিকোয়েন্স ক্যালকুলেটর
- ফিবোনাচি ফাংশনের সি ++ কোড
ফিবোনাচি সিকোয়েন্স সূত্র
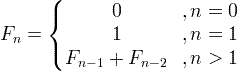
উদাহরণ স্বরূপ:
এফ 0 = 0
এফ 1 = 1
এফ 2 = এফ 1 + এফ 0 = 1 + 0 = 1
এফ 3 = এফ 2 + এফ 1 = 1 + 1 = 2
এফ 4 = এফ 3 + এফ 2 = 2 + 1 = 3
এফ 5 = এফ 4 + এফ 3 = 3 + 2 = 5
...
গোল্ডেন রেশিও কনভার্জেন্স
দুটি ক্রমযুক্ত ফিবোনাচি সংখ্যার অনুপাত স্বর্ণের অনুপাতে রূপান্তরিত করে:
![]()
φ হ'ল সোনার অনুপাত = (1 + ) 5 ) / 2 ≈ 1.61803399
ফিবোনাচি সিকোয়েন্স টেবিল
| এন | এফ এন |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 5 |
| 6 | 8 |
| 7 | 13 |
| 8 | 21 |
| 9 | 34 |
| 10 | 55 |
| 11 | 89 |
| 12 | 144 |
| 13 | 233 |
| 14 | 377 |
| 15 | 610 |
| 16 | 987 |
| 17 | 1597 |
| 18 | 2584 |
| 19 | 4181 |
| 20 | 6765 |
ফিবোনাচি সিকোয়েন্স ক্যালকুলেটর
টিবিডি
ফিবোনাচি ফাংশনের সি কোড
double Fibonacci(unsigned int n)
{
double f_n =n;
double f_n1=0.0;
double f_n2=1.0;
if( n / 1 ) {
for(int k=2; k<=n; k++) {
f_n = f_n1 + f_n2;
f_n2 = f_n1;
f_n1 = f_n;
}
}
return f_n;
}