ই ধ্রুবক
e ধ্রুবক বা uleলারের সংখ্যাটি গাণিতিক ধ্রুবক। ই ধ্রুবকটি আসল এবং অযৌক্তিক সংখ্যা।
e = 2.718281828459 ...
ই সংজ্ঞা
ই ধ্রুবক সীমা হিসাবে সংজ্ঞায়িত করা হয়:
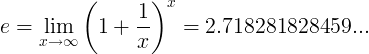
বিকল্প সংজ্ঞা
ই ধ্রুবক সীমা হিসাবে সংজ্ঞায়িত করা হয়:
![]()
ই ধ্রুবক অসীম সিরিজ হিসাবে সংজ্ঞায়িত করা হয়:
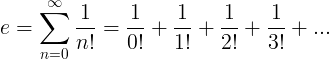
ই এর বৈশিষ্ট্য
ই এর পারস্পরিক
ই এর পারস্পরিক ক্রিয়া সীমা:
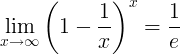
ই এর ডেরিভেটিভস
সূচকীয় ফাংশনের ডেরাইভেটিভ হ'ল এক্সফেনশনিয়াল ফাংশন:
( e x ) '= ই x
প্রাকৃতিক লোগারিদম ফাংশনের ডেরাইভেটিভ হ'ল পারস্পরিক ক্রিয়াকলাপ:
(লগ ই এক্স ) '= (এলএন এক্স )' = 1 / এক্স
ই এর সংহত
এর সূচকীয় ফাংশন ই অনির্দিষ্ট অবিচ্ছেদ্য এক্স সূচকীয় ফাংশন ই হয় এক্স ।
∫ ই এক্স DX = ই এক্স + C
প্রাকৃতিক লোগারিদম ফাংশন লগ ই এক্স এর অনির্দিষ্ট অবিচ্ছেদ্য হয়:
∫ লগ ই x ডিএক্স = ∫ এলএন এক্স ডিএক্স = এক্স এলএন এক্স - এক্স + সি
পারস্পরিক ক্রিয়াকলাপ 1 / x এর 1 থেকে e এর নির্দিষ্ট অবিচ্ছেদ্য 1:
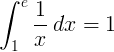
বেস ই লোগারিদম
একটি সংখ্যা x এর প্রাকৃতিক লোগারিদমকে x এর বেস এবং লোগারিদম হিসাবে সংজ্ঞায়িত করা হয়:
ln x = লগ ই x
ব্যাখ্যামূলক কাজ
সূচকীয় ফাংশনটি হিসাবে সংজ্ঞায়িত করা হয়:
f ( x ) = exp ( x ) = e x
ইউলারের সূত্র
জটিল নম্বর এবং আইটির পরিচয় রয়েছে:
e iθ = cos ( θ ) + আমি পাপ ( θ )
আমি কাল্পনিক ইউনিট (-1 এর বর্গমূল)।
any হ'ল যে কোনও আসল সংখ্যা।
আরো দেখুন
- কিভাবে ই 2.71828183?
- লোগারিদম বিধি
- প্রাকৃতিক লোগারিদম
- বিলোপকারীদের বিধি
- স্বাভাবিক বন্টন
- পাই ধ্রুবক
- ই ধ্রুব - উইকিপিডিয়া