অভিযোজক বিধি

অভিব্যক্তির বিধি, ঘাঁটিঘাঁটি আইন এবং উদাহরণ।

একটি অভিজাত কি

N এর শক্তিতে উত্থিত বেসটি a, n বারের গুণনের সমান:

a n = a × a × ... × a

                    n বার

a হল বেস এবং n হ'ল ঘ।

উদাহরণ

3 1 = 3

3 2 = 3 × 3 = 9

3 3 = 3 × 3 × 3 = 27

3 4 = 3 × 3 × 3 × 3 = 81

3 5 = 3 × 3 × 3 × 3 × 3 = 243

বিলোপকারীদের বিধি এবং বৈশিষ্ট্য

বিধি নাম নিয়ম উদাহরণ
পণ্য বিধি a n ⋅ a m = a n + m 2 3 ⋅ 2 4 = 2 3 + 4 = 128
a n ⋅ b n = ( a ⋅ b ) n 3 2 ⋅ 4 2 = (3⋅4) 2 = 144
কোটারিয়েন্ট বিধি a n / a m = a n - m 2 5 /2 3 = 2 5-3 = 4
a n / b n = ( a / b ) n 4 3 /2 3 = (4/2) 3 = 8
পাওয়ার বিধি ( b n ) m = b n⋅m (2 3 ) 2 = 2 3⋅2 = 64
বি এন এম = বি ( এন এম ) 2 3 2 = 2 ( 3 2 ) = 512
মি √ ( বি এন ) = বি এন / এম 2 √ (2 6 ) = 2 6/2 = 8
খ 1 / এন = এন √ বি 8 1/3 = 3 √ 8 = 2
নেতিবাচক উদ্দীপক বি- এন = 1 / বি এন 2 -3 = 1/2 3 = 0.125
শূন্য বিধি খ 0 = 1 5 0 = 1
0 এন = 0, এন / 0 এর জন্য 0 5 = 0
একটি নিয়ম খ 1 = খ 5 1 = 5
1 এন = 1 1 5 = 1
বিয়োগ একটি নিয়ম 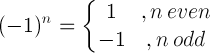(-1) 5 = -1
ডেরিভেটিভ বিধি ( x n ) ' = n ⋅ x n -1 ( x 3 ) ' = 3⋅ x 3-1
অবিচ্ছেদ্য নিয়ম ∫ x n dx = x n +1 / ( n +1) + C ∫ x 2 dx = x 2 + 1 / (2 + 1) + সি

এক্সটেনশন পণ্য বিধি

একই বেস সহ পণ্য বিধি

a n ⋅ a m = a n + m

উদাহরণ:

2 3 ⋅ 2 4 = 2 3 + 4 = 2 7 = 2⋅2⋅2⋅2⋅2⋅2⋅2 = 128

একই ব্যয়কারীর সাথে পণ্যের বিধি

a n ⋅ b n = ( a ⋅ b ) n

উদাহরণ:

3 2 ⋅ 4 2 = (3⋅4) 2 = 12 2 = 12⋅12 = 144

দেখুন: বহুগুণ বহনকারীকে

এক্সটেনার্স কোটারেন্ট বিধি

একই বেস সহ কোটারিয়েন্ট নিয়ম

a n / a m = a n - m

উদাহরণ:

2 5 /2 3 = 2 5-3 = 2 2 = 2⋅2 = 4

একই ব্যয়কারী সহ কোটারিয়েন্ট নিয়ম

a n / b n = ( a / b ) n

উদাহরণ:

4 3 /2 3 = (4/2) 3 = 2 3 = 2⋅2⋅2 = 8

দেখুন: বিভক্তকারীদের ভাগ করা

এক্সপোজার শক্তি বিধি

পাওয়ার বিধি আই

( a n ) m = a n⋅m

উদাহরণ:

(2 3 ) 2 = 2 3⋅2 = 2 6 = 2⋅2⋅2⋅2⋅2⋅2 = 64

ক্ষমতার বিধি II

a n m = a ( n m )

উদাহরণ:

2 3 2 = 2 (3 2 ) = 2 (3⋅3) = 2 9 = 2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2 = 512

র‌্যাডিক্যালসের সাথে পাওয়ার রুল

মি √ ( একটি এন ) = একটি এন / এম

উদাহরণ:

2 √ (2 6 ) = 2 6/2 = 2 3 = 2⋅2⋅2 = 8

নেতিবাচক উদ্বেগকারীদের বিধি

বি- এন = 1 / বি এন

উদাহরণ:

2 -3 = 1/2 3 = 1 / (2⋅2⋅2) = 1/8 = 0.125

দেখুন: gণাত্মক উদ্দীপক

 

এক্সপোনেন্ট ক্যালকুলেটর ►

 

আরো দেখুন

সংখ্যা
দ্রুত টেবিল