শূন্য নম্বর (0)
শূন্য সংখ্যা সংজ্ঞা
শূন্য কোনও সংখ্যা বা নাল পরিমাণের বর্ণনা দিতে গণিতে ব্যবহৃত একটি সংখ্যা।
যখন টেবিলে 2 টি আপেল থাকে এবং আমরা 2 টি আপেল নিই, আমরা বলতে পারি যে টেবিলে শূন্য আপেল রয়েছে।
শূন্য সংখ্যাটি ধনাত্মক সংখ্যা নয় এবং negativeণাত্মক সংখ্যা নয়।
শূন্যটি অন্য সংখ্যায় (যেমন: 40,103, 170) একটি স্থানধারক অঙ্ক।
শূন্য একটি সংখ্যা?
শূন্য একটি সংখ্যা। এটি ইতিবাচক বা নেতিবাচক সংখ্যা নয়।
জিরো ডিজিট
সংখ্যা লেখার সময় শূন্য অঙ্কটি স্থানধারক হিসাবে ব্যবহৃত হয়।
উদাহরণ স্বরূপ:
204 = 2 × 100 + 0 × 10 + 4 × 1
শূন্য নম্বর ইতিহাস
শূন্য সংখ্যাটি আবিষ্কার করেন কে?
আধুনিক 0 টি প্রতীকটি India-শতকে ভারতে উদ্ভাবিত হয়েছিল, পরে পার্সিয়ান এবং আরব এবং পরে ইউরোপে ব্যবহৃত হয়েছিল।
শূন্যের প্রতীক
শূন্য সংখ্যা 0 টি প্রতীক দিয়ে চিহ্নিত করা হয় ।
আরবি সংখ্যা সিস্টেমটি ٠ চিহ্ন ব্যবহার করে।
শূন্য নম্বর বৈশিষ্ট্য
এক্স যে কোনও সংখ্যার প্রতিনিধিত্ব করে।
| অপারেশন | নিয়ম | উদাহরণ |
|---|---|---|
সংযোজন |
x + 0 = x |
3 + 0 = 3 |
বিয়োগ |
x - 0 = x |
3 - 0 = 3 |
গুণ |
x × 0 = 0 |
5 × 0 = 0 |
বিভাগ |
0 ÷ x = 0 , যখন x ≠ 0 |
0 ÷ 5 = 0 |
| x ÷ 0 অপরিশোধিত |
5 ÷ 0 অপরিশোধিত |
|
ঘৃণা |
0 x = 0 |
0 5 = 0 |
| x 0 = 1 |
5 0 = 1 |
|
রুট |
√ 0 = 0 |
|
লোগারিদম |
লগ বি (0) নির্ধারিত |
|
| |
||
কারখানা |
0! = 1 |
|
সাইন |
sin 0º = 0 |
|
কোসিন |
কোস 0º = 1 |
|
স্পর্শকাতর |
ট্যান 0º = 0 |
|
অমৌলিক |
0 '= 0 |
|
ইন্টিগ্রাল |
∫ 0 ডি x x 0 0 সে |
|
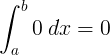 |
শূন্য সংযোজন
একটি সংখ্যার যোগ শূন্যের সংখ্যার সমান:
x + 0 = x
উদাহরণ স্বরূপ:
5 + 0 = 5
জিরো বিয়োগ
একটি সংখ্যা বিয়োগ শূন্যের বিয়োগটি সংখ্যার সমান:
x - 0 = x
উদাহরণ স্বরূপ:
5 - 0 = 5
শূন্য দ্বারা গুণ
একটি শূন্যের শূন্যের সমান গুণফল:
x × 0 = 0
উদাহরণ স্বরূপ:
5 × 0 = 0
শূন্য দ্বারা বিভক্ত সংখ্যা
শূন্য দ্বারা একটি সংখ্যার বিভাগ সংজ্ঞায়িত করা হয় না:
x ÷ 0 অপরিশোধিত
উদাহরণ স্বরূপ:
5 ÷ 0 অপরিশোধিত
শূন্য একটি সংখ্যা দ্বারা বিভক্ত
একটি সংখ্যা দ্বারা শূন্যের বিভাগ শূন্য:
0 ÷ x = 0
উদাহরণ স্বরূপ:
0 ÷ 5 = 0
শূন্য শক্তি সংখ্যা
শূন্য দ্বারা উত্থাপিত সংখ্যার শক্তি এক:
x 0 = 1
উদাহরণ স্বরূপ:
5 0 = 1
শূন্যের লোগারিদম
শূন্যের বেস বি লোগারিদম অপরিজ্ঞাত:
লগ বি (0) নির্ধারিত
শূন্য পাওয়ার জন্য আমরা বেস বি বাড়িয়ে নিতে পারি এমন কোনও সংখ্যা নেই।
X এর বেস বি লোগারিদমের কেবলমাত্র সীমা, যখন x শূন্য রূপান্তরিত হয় বিয়োগ অনন্ত:
![]()
শূন্য রয়েছে এমন সেটগুলি
জিরো প্রাকৃতিক সংখ্যা, পূর্ণসংখ্যার সংখ্যা, আসল সংখ্যা এবং জটিল সংখ্যা সেটগুলির একটি উপাদান:
| সেট | সদস্যপদ স্বরলিপি সেট করুন |
|---|---|
| প্রাকৃতিক সংখ্যা (নেতিবাচক নয়) | 0 ∈ ℕ 0 |
| পূর্ণসংখ্যার সংখ্যা | 0 ∈ ℤ |
| বাস্তব সংখ্যার | 0 ∈ ℝ |
| জটিল সংখ্যা | 0 ∈ ℂ |
| মূলদ সংখ্যা | 0 ∈ ℚ |
শূন্য সমান বা বিজোড় সংখ্যা?
সমান সংখ্যার সেটটি হ'ল:
{..., -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ...}
বিজোড় সংখ্যাগুলির সেটটি হ'ল:
{..., -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, ...}
জিরো 2 এর পূর্ণসংখ্যা একক:
0 × 2 = 0
শূন্য সমান সংখ্যাগুলির একটি সদস্য:
0 ∈ {2 কে , কে ∈ℤ}
সুতরাং শূন্য একটি বিজোড় সংখ্যা নয় একটি সমান সংখ্যা।
শূন্য কি প্রাকৃতিক সংখ্যা?
প্রাকৃতিক সংখ্যা সেট জন্য দুটি সংজ্ঞা আছে।
অ নেতিবাচক পূর্ণসংখ্যার সেট:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
ধনাত্মক পূর্ণসংখ্যার সেট:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
জিরো অ নেতিবাচক পূর্ণসংখ্যার সংস্থার একটি সদস্য:
0 ∈ ℕ 0
জিরো ধনাত্মক পূর্ণসংখ্যার সেটটির সদস্য নয়:
0 ∉ ℕ 1
শূন্য কি পুরো সংখ্যা?
পুরো সংখ্যার জন্য তিনটি সংজ্ঞা রয়েছে:
পূর্ণসংখ্যার সংখ্যার সেট:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
অ নেতিবাচক পূর্ণসংখ্যার সেট:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
ধনাত্মক পূর্ণসংখ্যার সেট:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
শূন্য পূর্ণসংখ্যার সংখ্যার সেট এবং অ নেতিবাচক পূর্ণসংখ্যার সেটগুলির একটি সদস্য:
0 ∈ ℤ
0 ∈ ℕ 0
জিরো ধনাত্মক পূর্ণসংখ্যার সেটটির সদস্য নয়:
0 ∉ ℕ 1
শূন্য একটি পূর্ণসংখ্যা সংখ্যা?
পূর্ণসংখ্যার সংখ্যার সেট:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
জিরো পূর্ণসংখ্যার সংখ্যার সেটের একজন সদস্য:
0 ∈ ℤ
সুতরাং শূন্য একটি পূর্ণসংখ্যা সংখ্যা।
শূন্য কি যুক্তিযুক্ত সংখ্যা?
যৌক্তিক সংখ্যাটি এমন একটি সংখ্যা যা দুটি পূর্ণসংখ্যার সংখ্যার ভাগফল হিসাবে প্রকাশ করা যায়:
ℚ = { n / এম ; এন , এম ∈ℤ}
শূন্য দুটি পূর্ণসংখ্যার সংখ্যার ভাগ হিসাবে লেখা যেতে পারে।
উদাহরণ স্বরূপ:
0 = 0/3
সুতরাং শূন্য একটি যুক্তিযুক্ত সংখ্যা।
শূন্য কি ধনাত্মক সংখ্যা?
ধনাত্মক সংখ্যাটি শূন্যের চেয়ে বৃহত একটি সংখ্যা হিসাবে সংজ্ঞায়িত করা হয়:
x / 0
উদাহরণ স্বরূপ:
5/ 0
যেহেতু শূন্য শূন্যের চেয়ে বড় নয়, এটি কোনও ধনাত্মক সংখ্যা নয়।
শূন্য কি মৌলিক সংখ্যা?
0 নম্বরটি কোনও মৌলিক সংখ্যা নয়।
শূন্য একটি ধনাত্মক সংখ্যা নয় এবং এতে বিভাজকের অসীম সংখ্যা রয়েছে।
সর্বনিম্ন মৌলিক সংখ্যা 2।