Equació quadràtica
L’equació quadràtica és un polinomi de segon ordre amb 3 coeficients: a , b , c .
L'equació quadràtica ve donada per:
ax 2 + bx + c = 0
La solució a l’equació quadràtica ve donada per 2 nombres x 1 i x 2 .
Podem canviar l’equació de segon grau a la forma de:
( x - x 1 ) ( x - x 2 ) = 0
Fórmula quadràtica
La solució a l’equació quadràtica ve donada per la fórmula quadràtica:
![]()
L'expressió dins de l'arrel quadrada s'anomena discriminant i es denota per by:
Δ = b 2 - 4 ac
La fórmula quadràtica amb notació discriminant:
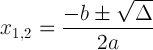
Aquesta expressió és important perquè ens pot explicar la solució:
- Quan Δ/ 0, hi ha 2 arrels reals x 1 = (- b + √ Δ ) / (2a) i x 2 = (- b-√ Δ ) / (2a) .
- Quan Δ = 0, hi ha una arrel x 1 = x 2 = -b / (2a) .
- Quan Δ <0, no hi ha arrels reals, hi ha 2 arrels complexes:
x 1 = (- b + i√ -Δ ) / (2a) i x 2 = (- bi√ -Δ ) / (2a) .
Problema núm. 1
3 x 2 +5 x +2 = 0
solució:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
Problema núm. 2
3 x 2 -6 x +3 = 0
solució:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
Problema núm. 3
x 2 +2 x +5 = 0
solució:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
No hi ha solucions reals. Els valors són nombres complexos:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
Gràfic de funcions quadràtiques
La funció quadràtica és una funció polinòmica de segon ordre:
f ( x ) = ax 2 + bx + c
Les solucions a l’equació quadràtica són les arrels de la funció quadràtica, que són els punts d’intersecció del gràfic de funció quadràtica amb l’eix x, quan
f ( x ) = 0
Quan hi ha 2 punts d’intersecció del gràfic amb l’eix x, hi ha 2 solucions a l’equació quadràtica.
Quan hi ha 1 punt d'intersecció del gràfic amb l'eix x, hi ha 1 solució a l'equació quadràtica.
Quan no hi ha punts d’intersecció del gràfic amb l’eix x, no obtenim solucions reals (ni 2 solucions complexes).