Regles del logaritme
El logaritme de la base b d’un nombre és l’ exponent que necessitem per elevar la base per obtenir el nombre.
- Definició del logaritme
- Regles del logaritme
- Problemes de logaritme
- Logaritme complex
- Gràfic del registre (x)
- Taula de logaritmes
- Calculadora de logaritmes
Definició del logaritme
Quan b s'eleva a la potència de y és igual a x:
b y = x
Llavors, el logaritme de la base b de x és igual a y:
log b ( x ) = y
Per exemple, quan:
2 4 = 16
Llavors
registre 2 (16) = 4
Logaritme com a funció inversa de la funció exponencial
La funció logarítmica,
y = registre b ( x )
és la funció inversa de la funció exponencial,
x = b y
Per tant, si calculem la funció exponencial del logaritme de x (x/ 0),
f ( f -1 ( x )) = b log b ( x ) = x
O si calculem el logaritme de la funció exponencial de x,
f -1 ( f ( x )) = log b ( b x ) = x
Logaritme natural (ln)
El logaritme natural és un logaritme de la base e:
ln ( x ) = registre e ( x )
Quan e constant és el nombre:
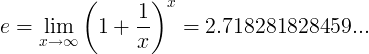
o
![]()
Vegeu: Logaritme natural
Càlcul del logaritme invers
El logaritme invers (o anti logaritme) es calcula elevant la base b al logaritme y:
x = log -1 ( y ) = b y
Funció logarítmica
La funció logarítmica té la forma bàsica de:
f ( x ) = registre b ( x )
Regles del logaritme
| Nom de la regla | Regla |
|---|---|
Regla de producte del logaritme |
log b ( x ∙ y ) = log b ( x ) + log b ( y ) |
Regla del quocient del logaritme |
log b ( x / y ) = log b ( x ) - log b ( y ) |
Regla de poder del logaritme |
log b ( x y ) = y ∙ log b ( x ) |
Regla de commutador de base de logaritme |
registre b ( c ) = 1 / registre c ( b ) |
Regla de canvi de base del logaritme |
log b ( x ) = log c ( x ) / log c ( b ) |
Derivada del logaritme |
f ( x ) = log b ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( b )) |
Integral del logaritme |
∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C |
Logaritme de nombre negatiu |
el registre b ( x ) no està definit quan x ≤ 0 |
Logaritme de 0 |
el registre b (0) no està definit |
Logaritme d'1 |
registre b (1) = 0 |
Logaritme de la base |
registre b ( b ) = 1 |
Logaritme de l’infinit |
lim log b ( x ) = ∞, quan x → ∞ |
Vegeu: Regles del logaritme
Regla de producte del logaritme
El logaritme de la multiplicació de x i y és la suma del logaritme de x i del logaritme de y.
log b ( x ∙ y ) = log b ( x ) + log b ( y )
Per exemple:
registre 10 (3 ∙ 7) = registre 10 (3) + registre 10 (7)
Regla del quocient del logaritme
El logaritme de la divisió de x i y és la diferència del logaritme de x i del logaritme de y.
log b ( x / y ) = log b ( x ) - log b ( y )
Per exemple:
log 10 (3 / 7) = log 10 (3) - log 10 (7)
Regla de poder del logaritme
El logaritme de x elevat a la potència de y és y vegades el logaritme de x.
log b ( x y ) = y ∙ log b ( x )
Per exemple:
registre 10 (2 8 ) = 8 ∙ registre 10 (2)
Regla de commutador de base de logaritme
El logaritme de la base b de c és 1 dividit pel logaritme de la base c de b.
registre b ( c ) = 1 / registre c ( b )
Per exemple:
registre 2 (8) = 1 / registre 8 (2)
Regla de canvi de base del logaritme
El logaritme de la base b de x és el logaritme de la base c de x dividit pel logaritme de la base c de b.
log b ( x ) = log c ( x ) / log c ( b )
Per exemple, per calcular el registre 2 (8) a la calculadora, hem de canviar la base a 10:
registre 2 (8) = registre 10 (8) / registre 10 (2)
Vegeu: regla de canvi de base de registre
Logaritme de nombre negatiu
El logaritme real de base b de x quan x <= 0 no està definit quan x és negatiu o igual a zero:
el registre b ( x ) no està definit quan x ≤ 0
Vegeu: registre del nombre negatiu
Logaritme de 0
El logaritme de base b de zero no està definit:
el registre b (0) no està definit
El límit del logaritme de base b de x, quan x s'aproxima a zero, és menys infinit:
![]()
Vegeu: registre de zero
Logaritme d'1
El logaritme base b d’un és zero:
registre b (1) = 0
Per exemple, el logaritme de la base dos d'un és zero:
registre 2 (1) = 0
Vegeu: registre d’un
Logaritme de l’infinit
El límit del logaritme de la base b de x, quan x s'aproxima a l'infinit, és igual a l'infinit:
lim log b ( x ) = ∞, quan x → ∞
Vegeu: registre de l’infinit
Logaritme de la base
El logaritme base b de b és un:
registre b ( b ) = 1
Per exemple, el logaritme de dos base de dos és un:
registre 2 (2) = 1
Derivada del logaritme
Quan
f ( x ) = registre b ( x )
Llavors la derivada de f (x):
f ' ( x ) = 1 / ( x ln ( b ))
Vegeu: derivada de registre
Integral de logaritme
La integral del logaritme de x:
∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C
Per exemple:
∫ log 2 ( x ) dx = x ∙ (log 2 ( x ) - 1 / ln (2) ) + C
Aproximació del logaritme
registre 2 ( x ) ≈ n + ( x / 2 n - 1),
Logaritme complex
Per al nombre complex z:
z = re iθ = x + iy
El logaritme complex serà (n = ...- 2, -1,0,1,2, ...):
Registre z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))
Problemes i respostes de logaritme
Problema núm. 1
Cerca x per
log 2 ( x ) + log 2 ( x -3) = 2
Solució:
Ús de la regla del producte:
log 2 ( x ∙ ( x -3)) = 2
Canvi del formulari de logaritme segons la definició de logaritme:
x ∙ ( x -3) = 2 2
O
x 2 -3 x -4 = 0
Resolució de l'equació de segon grau:
x 1,2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4, -1
Com que el logaritme no està definit per a nombres negatius, la resposta és:
x = 4
Problema núm. 2
Cerca x per
registre 3 ( x +2) - registre 3 ( x ) = 2
Solució:
Utilitzant la regla del quocient:
registre 3 (( x +2) / x ) = 2
Canvi del formulari de logaritme segons la definició de logaritme:
( x +2) / x = 3 2
O
x +2 = 9 x
O
8 x = 2
O
x = 0,25
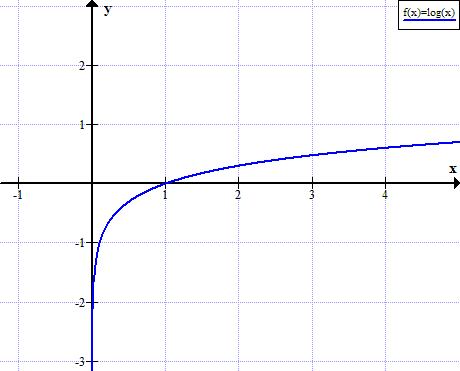
Gràfic del registre (x)
log (x) no està definit per a valors reals no positius de x:
Taula de logaritmes
| x | registre 10 x | registre 2 x | log e x |
|---|---|---|---|
| 0 | sense definir | sense definir | sense definir |
| 0 + | - ∞ | - ∞ | - ∞ |
| 0,0001 | -4 | -13.287712 | -9.210340 |
| 0,001 | -3 | -9,965784 | -6.907755 |
| 0,01 | -2 | -6,643856 | -4.605170 |
| 0,1 | -1 | -3.321928 | -2.302585 |
| 1 | 0 | 0 | 0 |
| 2 | 0,301030 | 1 | 0,693147 |
| 3 | 0,471212 | 1.584963 | 1.098612 |
| 4 | 0,602060 | 2 | 1.386294 |
| 5 | 0,698970 | 2.321928 | 1.609438 |
| 6 | 0,777151 | 2.584963 | 1.791759 |
| 7 | 0,845098 | 2.807355 | 1.945910 |
| 8 | 0,903090 | 3 | 2.079442 |
| 9 | 0,954243 | 3.169925 | 2.197225 |
| 10 | 1 | 3.321928 | 2.302585 |
| 20 | 1.301030 | 4.321928 | 2.995732 |
| 30 | 1.477121 | 4.906891 | 3.401197 |
| 40 | 1.602060 | 5.321928 | 3.688879 |
| 50 | 1.698970 | 5.643856 | 3.912023 |
| 60 | 1.778151 | 5.906991 | 4.094345 |
| 70 | 1.845098 | 6.129283 | 4.248495 |
| 80 | 1.903090 | 6.321928 | 4.382027 |
| 90 | 1.954243 | 6.491853 | 4.499810 |
| 100 | 2 | 6.643856 | 4.605170 |
| 200 | 2.301030 | 7.643856 | 5.298317 |
| 300 | 2.477121 | 8.228819 | 5.703782 |
| 400 | 2.602060 | 8.643856 | 5,991465 |
| 500 | 2.698970 | 8.965784 | 6.214608 |
| 600 | 2.778151 | 9.228819 | 6.396930 |
| 700 | 2.845098 | 9.451211 | 6.551080 |
| 800 | 2.903090 | 9.643856 | 6.684612 |
| 900 | 2.954243 | 9.813781 | 6,802395 |
| 1.000 | 3 | 9.965784 | 6,907755 |
| 10000 | 4 | 13.287712 | 9.210340 |
Vegeu també
- Regles del logaritme
- Canvi de base de logaritme
- Logaritme de zero
- Logaritme d’un
- Logaritme de l’infinit
- Logaritme de nombre negatiu
- Calculadora de logaritmes
- Gràfic de logaritme
- Taula de logaritmes
- Calculadora de logaritmes naturals
- Logaritme natural - ln x
- e constant
- Decibels (dB)