Logaritme natural - ln (x)
El logaritme natural és el logaritme de la base e d’un nombre.
- Definició de logaritme natural (ln)
- Regles i propietats del logaritme natural (ln)
- Logaritme complex
- Gràfic de ln (x)
- Taula de logaritmes naturals (ln)
- Calculadora de logaritmes naturals
Definició de logaritme natural
Quan
e y = x
Llavors la base e logaritme de x és
ln ( x ) = log e ( x ) = y
La constant e o número d'Euler és:
e ≈ 2.71828183
Ln com a funció inversa de la funció exponencial
La funció de logaritme natural ln (x) és la funció inversa de la funció exponencial e x .
Per a x/ 0,
f ( f -1 ( x )) = e ln ( x ) = x
O
f -1 ( f ( x )) = ln ( e x ) = x
Regles i propietats del logaritme natural
| Nom de la regla | Regla | Exemple |
|---|---|---|
Regla del producte |
ln ( x ∙ y ) = ln ( x ) + ln ( y ) |
ln (3 ∙ 7) = ln (3) + ln (7) |
Regla del quocient |
ln ( x / y ) = ln ( x ) - ln ( y ) |
ln (3 / 7) = ln (3) - ln (7) |
Regla de poder |
ln ( x y ) = y ∙ ln ( x ) |
ln (2 8 ) = 8 ∙ ln (2) |
En derivat |
f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x | |
Integral |
∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C | |
ln de nombre negatiu |
ln ( x ) no està definit quan x ≤ 0 | |
ln de zero |
ln (0) no està definit | |
ln d'un |
ln (1) = 0 | |
En l'infinit |
lim ln ( x ) = ∞, quan x → ∞ | |
| Identitat d'Euler | ln (-1) = i π |
Regla de producte del logaritme
El logaritme de la multiplicació de x i y és la suma del logaritme de x i del logaritme de y.
log b ( x ∙ y ) = log b ( x ) + log b ( y )
Per exemple:
registre 10 (3 ∙ 7) = registre 10 (3) + registre 10 (7)
Regla del quocient del logaritme
El logaritme de la divisió de x i y és la diferència del logaritme de x i del logaritme de y.
log b ( x / y ) = log b ( x ) - log b ( y )
Per exemple:
log 10 (3 / 7) = log 10 (3) - log 10 (7)
Regla de poder del logaritme
El logaritme de x elevat a la potència de y és y vegades el logaritme de x.
log b ( x y ) = y ∙ log b ( x )
Per exemple:
registre 10 (2 8 ) = 8 ∙ registre 10 (2)
Derivada del logaritme natural
La derivada de la funció de logaritme natural és la funció recíproca.
Quan
f ( x ) = ln ( x )
La derivada de f (x) és:
f ' ( x ) = 1 / x
Integral del logaritme natural
La integral de la funció de logaritme natural ve donada per:
Quan
f ( x ) = ln ( x )
La integral de f (x) és:
∫ f ( x ) dx = ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C
Ln de 0
El logaritme natural de zero no està definit:
ln (0) no està definit
El límit proper a 0 del logaritme natural de x, quan x s'aproxima a zero, és menys infinit:
![]()
Ln d'1
El logaritme natural d'un és zero:
ln (1) = 0
Ln d'infinit
El límit del logaritme natural de l'infinit, quan x s'aproxima a l'infinit, és igual a l'infinit:
lim ln ( x ) = ∞, quan x → ∞
Logaritme complex
Per al nombre complex z:
z = re iθ = x + iy
El logaritme complex serà (n = ...- 2, -1,0,1,2, ...):
Registre z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))
Gràfic de ln (x)
ln (x) no està definit per a valors reals no positius de x:
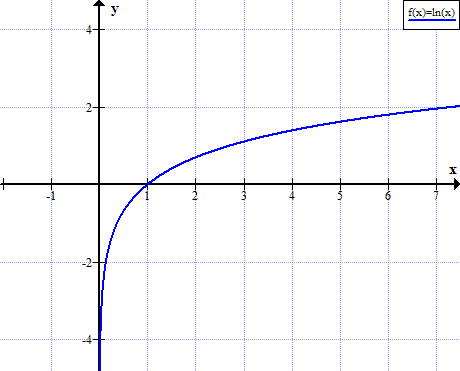
Taula de logaritmes naturals
| x | ln x |
|---|---|
| 0 | sense definir |
| 0 + | - ∞ |
| 0,0001 | -9.210340 |
| 0,001 | -6.907755 |
| 0,01 | -4.605170 |
| 0,1 | -2.302585 |
| 1 | 0 |
| 2 | 0,693147 |
| e ≈ 2.7183 | 1 |
| 3 | 1.098612 |
| 4 | 1.386294 |
| 5 | 1.609438 |
| 6 | 1.791759 |
| 7 | 1.945910 |
| 8 | 2.079442 |
| 9 | 2.197225 |
| 10 | 2.302585 |
| 20 | 2.995732 |
| 30 | 3.401197 |
| 40 | 3.688879 |
| 50 | 3.912023 |
| 60 | 4.094345 |
| 70 | 4.248495 |
| 80 | 4.382027 |
| 90 | 4.499810 |
| 100 | 4.605170 |
| 200 | 5.298317 |
| 300 | 5.703782 |
| 400 | 5,991465 |
| 500 | 6.214608 |
| 600 | 6.396930 |
| 700 | 6.551080 |
| 800 | 6.684612 |
| 900 | 6,802395 |
| 1.000 | 6,907755 |
| 10000 | 9.210340 |
Vegeu també
- Logaritme (registre)
- Calculadora de logaritmes naturals
- Logaritme natural de zero
- Logaritme natural d’un
- Logaritme natural d’e
- Logaritme natural de l’infinit
- Logaritme natural de nombre negatiu
- Ln funció inversa
- ln (x) gràfic
- Taula de logaritme natural
- Calculadora de logaritmes
- e constant
ÀLGEBRA
TAULES RÀPIDES